(zenodo.org)

Mail.ru

Correction dated 2025.06.20

An unfortunate error was discovered in the size scaling formula; however, a solution has been found which still leads to the desired result when scaling the size. Appendix 8, therefore, remains unchanged. The postulates have been slightly amended (specifically 3.3). The calculation in Appendix 8 for the scaling of the interaction speed has been corrected.

Annotation

This paper presents a theoretical model describing matter, fundamental interactions and the structure of the Universe on the basis of unified wave principles and the concept of fractality. The paper aims to overcome the fragmentation of modern physical theories by offering an alternative approach to explain the nature of mass, electric charge, gravitation and the origin of fundamental constants.

The model is based on the idea that elementary particles are stable standing waves formed in Euclidean space, considered as an energy-rich medium. Interactions between particles and formation of all fundamental forces are interpreted as a result of resonance processes in this medium. The existence of a longitudinal component of electromagnetic waves, which plays an important role in the structure of matter, is assumed.

A mathematical model has been developed that allows to derive the key parameters of the main stable elementary particles (neutrino, electron, neutron, proton), such as mass and characteristic wavelength, from the first principles of the model, based on the quantisation of standing wave knots and the fundamental speed of interaction (speed of light). A mechanism for the origin of the elementary electric charge as a characteristic of the geometrical work done by space in forming the half-wave of the particle is also proposed. The theoretically calculated values of masses and charge show good agreement with experimental data.

The model offers an explanation of the constancy of the speed of light and derives the Lorentz transformations as a consequence of the wave nature of matter and resonance interactions. Within the framework of the fractal structure of the Universe such phenomena as dark matter and dark energy are interpreted, and the scalability of matter properties is predicted (e.g., the correspondence between the parameters of the neutron and the Milky Way galaxy). Implications of the model for understanding quantum entanglement are discussed and testable predictions are offered, including the dependence of the half-life of the neutron on the density of surrounding matter.

The proposed approach does not deny the achievements of existing physics, but seeks to integrate them into a more general and intuitive picture of the world, where the fundamental properties of matter and laws of nature are a consequence of the unified wave dynamics of energy.

Keywords: wave model of matter, fractal Universe, resonance, standing waves, origin of mass and charge, fundamental constants, unified theory of interactions, longitudinal waves

1. Introduction

Contemporary fundamental physics, despite significant achievements in describing a wide array of phenomena, faces a number of conceptual challenges. Existing theories, such as quantum mechanics and general relativity, successfully describe reality at their respective scales; however, their complete unification into a single comprehensive system remains an unresolved task. The origin and precise values of fundamental physical constants, as well as the nature of such foundational concepts as mass, electric charge, and gravitation, continue to pose profound questions. Furthermore, the phenomena of dark matter and dark energy, which account for a significant portion of the Universe’s energy balance, indicate the incompleteness of our current understanding. There is also a lack of a universal approach capable of describing the structure of matter at all levels – from elementary particles to the cosmological scales of galaxies – based on a single principle.

Many modern models rely on complex, at times abstract, mathematical constructs, the physical meaning of which is not always evident. This complicates an intuitive grasp of the nature of observed phenomena and hinders the creation of a holistic worldview. The concepts of the ‘point particle’ and ‘wave function’ are effectively employed to describe experiments; however, the intrinsic nature of these ‘points’ and the mechanism underlying wave-like behaviour remain beyond direct observation and complete theoretical comprehension.

This work proposes an alternative approach, founded upon a wave model of matter and the principle of the fractal structure of the Universe. The key hypothesis is that matter at all levels consists of stable standing waves, forming within a unified energy-saturated medium (the physical vacuum). Interactions between these wave structures, encompassing all fundamental forces, are interpreted as manifestations of a universal mechanism – resonance. Observed ‘point particles’, in this context, are considered to be localised regions of these wave processes, whose internal structure may be concealed from us due to limitations imposed by the speed of our perception and the nature of interactions.

The primary objective of the present work is to develop and present a theoretical and mathematical model which, proceeding from these wave and fractal principles, is capable of:

• Describing the structure and properties of the principal stable elementary particles (neutrino, electron, neutron, proton).
• Proposing a mechanism for the origin of mass and electric charge as characteristics of wave structures.
• Providing an interpretation for fundamental physical constants.
• Explaining the nature of gravitation and other fundamental interactions via a unified resonant mechanism.
• Shedding light on phenomena such as quantum entanglement and the nature of the photon, as well as offering an explanation for the effects of dark matter and dark energy within the framework of fractal scaling.

The proposed approach does not seek to negate the achievements of contemporary physics but, on the contrary, aims to integrate them into a more general and physically intuitive conceptual system. Many established laws and models remain valid within their domains of applicability, whilst acquiring new meaning in the context of wave energy dynamics. This work is directed towards simplifying the understanding of the world’s structure, offering an intuitively clearer picture based on the universality of wave processes and resonant interactions, supported by mathematical calculations whose results are compared with experimental data.

2. Postulates

The following postulates serve as the foundation of the proposed theory of the wave model of matter and fractal structure of the Universe:

• The Primality of Energy and the Nature of Space:

1. Energy is the fundamental basis of all physical objects, phenomena and interactions. All things are different forms of manifestation and structurisation of energy.
2. Space is not a passive void, but is an active energy-rich medium, possessing structure and capable of supporting and transforming wave processes.

• Wave Nature of Matter and its Properties:

1. Matter is fundamentally stable standing waves formed in an energy-rich environment.
2. Four basic types of stable standing waves are assumed to exist, which correspond to the main stable elementary particles (neutrino, electron, neutron and proton).
3. The fundamental properties of particles, such as mass, electric charge and spin, are derived characteristics determined by the geometry, dynamics and stability of their wave structures.
4. The mass is determined by the amplitude of the longitudinal component of the standing wave and its half-wave structure.

• Mechanism of Interactions:

1. All interactions between particles and objects are carried out through resonance — the coordinated exchange of energy between wave structures.
2. The fundamental forces of nature (gravitational, electromagnetic, weak and strong) are different macroscopic manifestations of a single mechanism of resonance interactions in the energy medium.
3. Principle of Harmonic Resonance and Frequency Scaling:

• Interaction and self-similarity between different fractal levels are ensured by resonance. The condition for this inter-scale resonance is not the equality of frequencies, but their harmonic coherence.
• Each fractal series (for instance, our world) is characterised by a base frequency (ν₀​) at the zeroth level (n=0).
• When transitioning between fractal levels (n), this frequency scales according to a strict mathematical law (νₙ​=ν₀​⋅(ℏ_quant)²ⁿ​), preserving the harmonic coherence of the entire system.
• It is precisely this harmonic connection, rather than an equality of frequencies, that is the condition for inter-scale resonance and determines the dynamic characteristics (including the limiting interaction speed Cₙ​) at each level.

• The Geometry of Space and the Nature of Time:

1. Space at a fundamental level is Euclidean.
2. Changes in energy (its distribution and density) affect the formation and properties of wave formations (matter) in this space, but do not lead to curvature of Euclidean space itself.
3. Time is not an independent fundamental entity, but a manifestation of the sequence of changes of energy states and wave configurations in space.

• Structural and Interpretive Principles:

1. The structure of matter and the Universe is fractal: wave formations can be nested, exhibiting self-similar patterns at different scales.
2. The observed «pointness» of elementary particles is a consequence of the limitations of our perception and interaction due to the finite propagation speed of interactions and resonance conditions that lead to localisation of wave packets.
3. There is a unity of energy, its wave form and the process of perception. Everything we observe is a manifestation of the unified wave nature of energy. The differences between matter, field and interaction are due to the configuration, scale and frequency of standing waves. Observation is interpreted as active participation in a process of resonant alignment where the form of the object and the act of perception are mutually conditioned.

• Features of Electromagnetic Waves:

1. Electromagnetic waves have not only a transverse but also a longitudinal component, arising due to the finiteness of their propagation speed and the need for redistribution of energy in space. This longitudinal component plays an essential role in the formation of the structure of matter.

3. logical implications of the model

Proceeding from the formulated postulates regarding the primacy of energy, the wave nature of matter, the resonant character of interactions, Euclidean space, and fractality (as outlined in the Postulates section, e.g.,), a number of logical consequences emerge. These consequences form the conceptual basis for explaining fundamental physical phenomena and the properties of matter within the framework of the proposed model.

3.1 Consequences Pertaining to the Nature of Matter and its Fundamental Properties:

• Structure and Scale of Matter: Matter, being comprised of stable standing wave formations within an energy-saturated medium (as per Postulate 2.1), derives its spatial characteristics (particle sizes, distances, boundaries) directly from the parameters of these waves. Thus, the geometry of objects is not an external attribute but is intrinsically inherent to their wave structure.
• The Nature of Mass: Mass is interpreted not as an initially inherent property but as a manifestation of a stable wave process – specifically, as a characteristic linked to the amplitude of a longitudinal standing wave and the structure of its semi-waves (as per Postulates 2.3 and 2.3.1). An increase in the amplitude or complexity of the wave structure corresponds to an increase in mass.
• The Origin of Electric Charge: Electric charge arises as a specific characteristic of standing waves with an even number of nodes. It is associated with the invariant geometrical work performed by space in the formation of a particle’s boundary semi-wave. The constancy of this work for all elementary wave units, conditioned by resonant coupling in a unified space, explains the quantisation and invariability of the elementary charge.

3.2 Consequences Pertaining to Fundamental Interactions:

• Universal Mechanism of Interactions via Resonance: All fundamental forces – electromagnetic, weak, strong, and gravitational – are various manifestations of a single principle: the resonant exchange of energy between wave structures within an energetic medium (as per Postulates 3.1 and 3.2).
• The Nature of Gravitation: Gravitation in this model is not linked to the curvature of Euclidean space (as per Postulates 4.1 and 4.2) but arises as a reaction of the energetic medium of space to a local perturbation of energy density caused by the formation of mass (a standing wave).

3.3 Consequences Pertaining to General Principles of Organisation and Perception:

• Fractality as a Universal Organisational Principle: The postulate concerning the fractal structure of matter (as per Postulate 5.1) leads to the conclusion of self-similarity in wave formations at various scales. This implies that the regularities governing elementary particles may be reflected in the structure and dynamics of cosmological objects, such as galaxies, representing different levels of a unified fractal organisation.
• Invariance of Work and Conservation of Energy: The stability of material structures (standing waves) corresponds to states wherein the invariance of geometrical work is maintained amidst changes in configuration (e.g., the number of nodes). This principle, founded upon resonance, ensures the adherence to the law of conservation of energy in wave interactions.
• The Nature of Time: Time, in accordance with Postulate 4.3, is not an independent entity but is interpreted as our perceived manifestation of the sequence of changes in wave configurations and energetic states within space.
• Energy as a Universal State Parameter: Energy (as per Postulate 1.1) determines not only the possibility of motion or thermal state but also the very possibility of a structure’s existence, its form, mass, and capacity for interaction. Changes in energy determine the phase transitions and transformations of matter.

3.4 Consequences Pertaining to Dynamic Processes:

• Absorption and Emission of Energy: The processes of absorption and emission (e.g., the emission of a photon) are not regarded as the creation or annihilation of particles from nothing, but as a reconfiguration of the resonant states of wave structures. This involves a change in wave configuration, harmonised with the overall resonance of the system and the medium.

4. Reconciliation of theoretical calculations with observed values

To test the hypothesis, calculations of key parameters of elementary particles (neutrino, electron, neutron, proton) based on the wave model have been performed. The results were compared with experimentally measured values:

n	name	λ₀ (m)	M₀ (кг)	m₀ (kg)	d₀ (m)	λ₀ exp (m)	m₀exp (kg)	d₀exp (m)
1	neutrino	9,715‬×10⁻¹¹	2,663×10⁻³²	6,581×10⁻³⁷	9,715‬×10⁻¹¹	10⁻⁶	<2.2×10⁻³⁷	10⁻¹⁰
2	electron	2,83×10⁻¹²	9,149×10⁻³¹	9,149×10⁻³¹	4,244×10⁻¹²	2.43×10⁻¹²	9.109×10⁻³¹	10⁻¹⁸
3	neutron	8,241×10⁻¹⁴	3,142×10⁻²⁹	1,617‬×10⁻²⁷	1,648‬×10⁻¹³	10⁻¹⁵	1.675×10⁻²⁷	10⁻¹⁵
4	proton	2,4×10⁻¹⁵	1,078‬×10⁻²⁷	1,617‬×10⁻²⁷	6,001‬×10⁻¹⁵	1.32×10⁻¹⁵	1.673×10⁻²⁷	10⁻¹⁵

Notes:

• λ₀ is the characteristic wavelength from the model;
• M₀ is the amplitude of the wave;
• m₀ — resultant mass, depends on the amplitude of the wave and the number of half-waves associated with the centre point of the wave structure;
• d₀ is the calculated diameter (or radius) of the wave structure;
• «exp» — experimental values.

Elementary charge obtained in the model:

q₀ = 1.5506912… × 10⁻¹⁹ Cl,
which is comparable with the experimental value

e = 1.602176634 × 10⁻¹⁹ Cl — the error is less than 3.2%.

The obtained values of mass, wavelength, and radius agree well with the experimental ones, especially for the electron and proton. This confirms that standing waves in the medium can be the basis for the formation of stable particles and their properties.

The obtained value of the elementary charge is also close to the experimental one, which indicates the possibility of describing the electromagnetic interaction through the internal structure of the wave object.

5. Areas Where the Model Offers a More Holistic or Physically Intuitive Explanation:

The proposed wave model of matter and fractal structure of the Universe, based on the postulates outlined above, allows for new or more intuitive physical interpretations of a number of fundamental phenomena and concepts.

• Origin of Fundamental Interactions

In this model, all fundamental forces – gravitational, electromagnetic, strong, and weak – are interpreted not as initially distinct entities, but as different manifestations of a single universal mechanism: the resonant exchange of energy between wave structures within an energy-saturated medium. This follows directly from Postulate 3.2, which states that fundamental forces are macroscopic manifestations of resonant interactions, and Postulate 3.1, which posits resonance itself as the basis of all interactions.

• Explanation of the Nature of Mass

Mass, in this model, is not a primary, postulated property but is derived as a result of a stable wave process – specifically, as a characteristic linked to the amplitude of the longitudinal component of a standing wave and the structure of its semi-waves (in accordance with Postulate 2.3). The model also explains potential «mass jitter» in strong fields as a result of internal resonant transitions within the wave structure. The change in the effective value of mass in regions of altered energy density (as per Postulate 1.2) also finds its explanation, as mass is a consequence of the amplitude of energy oscillations (as per Postulate 1.1).

• Explanation of the Nature of Electric Charge

Electric charge is associated with the specific structure of standing waves, namely those that possess an even number of nodes. Its origin is interpreted as the result of invariant geometrical work performed by space (the energetic medium, according to Postulate 1.2) during the formation of a particle’s boundary semi-wave. This approach to charge as a derivative characteristic of a wave structure (as per Postulate 2.3) allows for an explanation of its quantisation and constancy.

• Explanation of the Photon’s Zero Rest Mass

The photon, in this model, is considered a wave structure with an asymmetric spherical form, distinguishing it from the standing waves that constitute massive particles. This asymmetry and the absence of a closed standing wave structure capable of retaining energy at rest in a manner analogous to particles with mass explain its zero rest mass and constant motion at the speed of light, which is a consequence of its specific wave configuration (in accordance with Postulate 2.3 concerning properties determined by wave geometry).

• Explanation of the Constancy of the Speed of Light

The limiting speed of interaction propagation (c) is explained not by the properties of an abstract ‘void’, but by the fact that stable resonance (as per Postulate 3.1) in an energetic medium (as per Postulate 1.2) is possible only at a certain fundamental frequency. This frequency determines the coherent exchange of energy and sets the ultimate speed of interaction (as per Postulate 3.3). The medium itself and its properties thus arise as a manifestation of this fundamental resonance.

• Origin of the Lorentz Transformations

The Lorentz transformations are derived in this model not as an initial postulate, but as a consequence of the wave nature of matter (as per Postulate 2.1) and the constancy of the speed of interactions, conditioned by the fundamental resonance of the medium (as per Postulate 3.3). Length contraction and time dilation for moving objects are interpreted as real changes in their wave structures.

• Wave Nature of Particles and Wave-Particle Duality

The standing wave model naturally explains wave-particle duality. A particle interacts locally (as a ‘point’) in the region of its nodes or maximum energy density, but its distribution in space and its behaviour in certain experiments (e.g., diffraction) are determined by its wave structure (as per Postulate 2.1). ‘Point-like’ behaviour, in this context, is a consequence of limited perception and interaction conditions (as per Postulate 5.2).

• Polarisation and Spin

These particle properties also find an explanation within the wave model. Polarisation is linked to the shape and orientation of the particle’s wave envelope. Spin can be interpreted either as a result of the distortion of the wave structure’s form relative to an ideal spherical shape (for charged particles) or as a manifestation of the internal rotation of energy density (for neutral particles with an odd number of nodes). Both aspects are characteristics of the geometry and dynamics of the wave structure (as per Postulate 2.3).

• Neutron Half-Life and Quantum Entanglement

The model proposes that neutral particles with an odd number of nodes (such as the neutron) are born in pairs with their antiparticles and are characterised by an internal rotation of energy, which leads to their quantum entanglement. The instability of the free neutron and its half-life are linked to this entangled state and its interaction with the surrounding energetic medium. It is suggested that the half-life may vary depending on the local concentration of matter (density of the energetic medium, according to Postulate 1.2), which influences the resonance conditions (as per Postulate 3.1).

• Dark Matter and Dark Energy

Observed effects attributed to dark matter and dark energy are interpreted in this model as manifestations of resonant interactions and density deformations of the energetic medium at larger, cosmological scales. This is a direct consequence of the Postulate of Fractality (Postulate 5.1), according to which galaxies can represent standing waves of energy at the corresponding fractal level.

• The Lamb Shift

This subtle effect in atomic spectra is explained as the result of the interaction of an electron (a wave structure, as per Postulate 2.1) with a local distortion of the energy density of space (as per Postulate 1.2), caused by the presence of a proton (a massive wave structure, as per Postulate 2.4). The closer the electron orbital is to the nucleus, the stronger this interaction, which leads to the shift in the energy level.

• Quantum Entanglement («Spooky Action at a Distance»)

Entanglement is interpreted as the coherent tuning of resonant systems (as per Postulate 3.1) within a unified energetic medium. For systems with internal energy rotation (such as neutral particles), the interaction can be directed ‘to a point’ (the centre of rotation), where the concept of distance in Euclidean space (as per Postulate 4.2) loses its usual meaning for this type of connection, thereby ensuring apparent instantaneity.

• Processes Beyond the Event Horizon of Black Holes

The event horizon is regarded as a boundary beyond which the energetic medium (as per Postulate 1.2) transitions into a state with a substantially different (increased) speed of interaction propagation (Postulate 3.3 allows for different speeds at different fractal levels). This may correspond to a transition to another fractal level (as per Postulate 5.1), where its own ‘Universe’ exists, perceived by us as a point or singularity.

• Reducibility of Classical and Quantum Physics

The wave model of matter (as per Postulate 2.1) inherently bridges the rigid gap between field continuity and particle discreteness. Particles are discrete, stable wave structures (quantum objects), but their interactions and propagation in the medium obey wave laws, which at the macroscopic level can lead to classical behaviour.

6. Model predictions

The proposed wave model of matter and fractal structure of the Universe allows for the formulation of a number of testable predictions, which can either confirm its main tenets or indicate the need for further refinements.

6.1. Fractal Correspondence of Scales: From Elementary Particles to Galaxies

• Essence of the Prediction: If the structure of the world is indeed fractal, as postulated in the model (Postulate 5.1), then analogies and scalable correspondences should be observed between objects at different levels of matter organisation. In particular, elementary particles, considered as standing waves of energy, may have structural and dynamic analogues on cosmological scales, for example, in the form of galaxies.
• Verification and Current Status: Appendix 8 («Scaling between the Neutron and the Milky Way») presents a calculation demonstrating that when scaling the parameters of a neutron (using fractal relationships derived in the model) to cosmological sizes, the obtained values for mass and size are close to the observed parameters of the Milky Way galaxy. The coincidence of several parameters simultaneously indicates that such a correspondence is non-random and can be considered indirect confirmation of the fractal principle. Further research could be directed towards finding similar correspondences for other types of particles and galaxies.

6.2. Influence of External Conditions on the Properties of Quantumly Entangled Particle Pairs (using the neutron and antineutron as an example)

• Essence of the Prediction: The model suggests that neutral particles with an odd number of nodes, such as the neutron, are born in pairs with their antiparticles (e.g., a neutron and an antineutron) and exist in a state of quantum entanglement, conditioned by their common wave nature and the conservation of characteristics (e.g., opposite directions of internal energy rotation). This entanglement means that the state of one particle is inextricably linked to the state of the other, irrespective of the distance between them. It is predicted that a targeted influence on one particle of such an entangled pair should lead to an instantaneous change in the measurable characteristics of the second particle.
• Experimental Verification:
  • It is necessary to develop a methodology that allows for the registration of neutron-antineutron pairs directly at the moment of their creation (e.g., in annihilation reactions or high-energy collisions) and to maintain them in isolated conditions, minimising external interactions.
  • Subsequently, a controlled influence (e.g., a magnetic field, a change in the density of the surrounding energetic medium) should be applied to one of the particles in the pair.
  • Simultaneously, precise measurements of the characteristics of the second particle must be conducted (e.g., its lifetime before decay, interaction parameters if it is stable under the given conditions, or characteristics of its own internal energy rotation, if measurable).
  • The detection of correlated changes in the second particle, synchronous with the influence on the first, would serve as confirmation of the predicted quantum entanglement and the mechanism of its influence on particle properties. The initial hypothesis regarding the dependence of the free neutron’s half-life on the density of the surrounding matter is a specific instance of this more general prediction, where the surrounding environment exerts an uncontrolled ‘influence’ on one of the components of the entangled system.

6.3. Dependence of the Fine-Structure Constant (α) on the Local Gravitational Potential

• Essence of the Prediction: The model posits that the fine-structure constant α is not a universal constant but may depend on the local energy density of space, which, in turn, is determined by the gravitational field of surrounding macro-objects. Thus, α could act as a «context-dependent» quantity.
• Experimental Verification: An experiment is proposed (described in section 7.6.4) to measure the electrostatic interaction force between two charged bodies whilst varying gravitational conditions (e.g., at different altitudes above sea level). A change in the equilibrium distance between the bodies (all other conditions being equal) could indicate a change in the effective charge and, consequently, a variability in α. The detection of statistically significant deviations would provide indirect confirmation of this hypothesis and of the influence of gravitation on electromagnetic interactions via α.

6.4. Resonant Frequencies of Macro-Objects and their Practical Application (using the Earth as an example)

• Essence of the Prediction/Consequence: This model allows for the calculation of a set of characteristic resonant frequencies for macro-objects, such as the Earth, based on their dimensions and the wave parameters derived in the theory. These frequencies correspond to different types of wave interactions (analogous to elementary particles with a varying number of nodes, n) with the given macro-object.
• Potential Applications:
  • Wireless Energy Transmission: Influencing a macro-object (e.g., the Earth) at one of its resonant frequencies, or multiples thereof, could allow for the transmission of energy over considerable distances without wires, using the medium itself (the Earth as a waveguide or resonator) to convey oscillations. This resonates with the ideas of Nikola Tesla.
  • Modification of Gravitational Interaction: If gravitation, according to this model, is a result of wave processes and resonance, then targeted influence at the resonant frequencies of a macro-object could theoretically lead to a local alteration of gravitational interaction.
  • Detection and Generation of Gravitational Waves/Seismic Activity: The model predicts that at certain frequencies (particularly for n>4), the interaction energy transitions into internal oscillations of the macro-object, which may manifest as seismic activity or the generation of gravitational waves. Monitoring emissions at these frequencies could serve to predict or detect such activity.

7. Mathematical model of the structure of elementary particles in space

Introduction

In this chapter, a mathematical apparatus is constructed, according to which elementary particles can be described through standing waves with different number of nodes. This allows us to relate their properties to scaling in space and interaction through wave resonance between fractal levels

To understand and justify what an elementary particle in space is, the paper devotes Appendices 1, 2 and 3. Appendix 6 states the principle of scalability (fractality) in space at finite propagation speed of interactions.

Under elementary particles in this paper we consider only four known, stable particles — neutrino, electron, neutron and proton, as well as their anti-analogues. It is assumed that only four stable stable standing waves in space can exist.

Despite the fact that the free neutron is not stable, within the framework of this model it is considered as a standing wave, under certain conditions preserving its integrity. Its half-life can be explained by its peculiarity of energy rotation within its structure, which leads to entanglement in the birth of neutron and antineutron. Since it is subject to frequent interactions due to its sufficient mass, a change in the state of one of the pair leads to a change in the state of the other.

It is assumed that the rule should be preserved — the smaller the wavelength, the higher the mass value. The larger the number of nodes, the smaller the wavelength, since we have a limited speed of propagation of interactions, the correspondingly higher the mass. This is an analogue of energy quantisation in standing waves, as in a string: energy increases with the number of nodes, while the length shortens.

It is known from experience that of the listed particles the electron and the proton have charge. In this work they should correspond to standing waves with an even number of nodes. Proceeding from this and from the known from experiments masses of particles, it is possible to assume sequences of particles in the order of increasing number of nodes of the standing wave — neutrino, electron, neutron and proton. Here only the neutron is out of the general picture. It is considered that its mass is greater than that of the proton, which based on this paper should not be. But taking into account that it has in its structure the effect of internal rotation of energy, which, when measuring the mass, in fact, is similar to the manifestation of charge between charged particles, it can lead to a misinterpretation of the obtained result. I.e., the neutron mass obtained in the experiment may be overestimated, and the interaction of rotational energy may be added to it, which leads to an overestimated mass value.

7.1 Relationship between dimensions and weight

7.1.1 Initial data:

To describe an elementary particle as a wave object, let us consider the interaction of two interrelated wave components, transverse and longitudinal. Their interaction is considered in the transverse section.

• Interaction velocity: It is taken equal to c (speed of light in vacuum).
• Wave propagation: A wave is considered to have components along two conventional orthogonal axes:
  • The x-axis: is responsible for the spatial dimension (longitudinal wave).
  • The y-axis: is responsible for the energy/mass characteristic (energy related transverse wave).
• Transverse component: This component is considered as a carrier of amplitude information related to the energy density. Through the formula E=mc² it allows to pass to the concept of mass.

Constancy of c²: Since the interaction velocity c is a constant, the value of c² becomes important. If a wave propagates simultaneously along the x and y axes with velocity components υₓ and υ_y respectively, then by Pythagoras’ theorem:

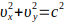
This relationship reflects the balance between the geometric (size) and energetic (mass) manifestations of the wave.

(Note: In this section, to simplify mathematical expressions and focus on numerical relationships, we will often omit physical dimensions by using numerical values of quantities. For example, c may refer to its numerical value in the SI system. Restoration of dimensions is a separate task).

7.1.2 Derivation of size and mass limits for standing waves

In order to form a stable standing wave, it is necessary that all its parts remain in interaction. This imposes restrictions on the maximum and minimum sizes of such wave formations and their associated masses.

A standing wave requires that all points of the wave can remain in interaction, i.e. the maximum distance between points must not exceed the path that the signal can travel in a given time. If we were to consider only the propagation of the wave along the x-axis, then at Δt≤ 1/c we would observe an interaction between the initial and final points of propagation. Since we consider propagation along two orthogonal directions, the interaction time limit is replaced by the condition Δt 1/≤| c²|ₙᵤₘ. which corresponds to the interaction limit when both the geometric (x) and energy (y) components are fully engaged.

In this case, we can speak about the maximum size of standing waves in the region of space, which will take place at once for both types of waves — transverse and longitudinal components. Their size cannot exceed the size:

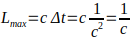
1. Limit dimensions (L):

We consider the propagation of the interaction along two orthogonal directions (size x and energy/mass y) where the total velocity is bounded by c.

• Maximum characteristic size (Lₘₐₓ): The largest size at which the standing wave components can effectively interact will not exceed

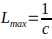
This corresponds to the case where the bulk of the «rate of change» is directed along the spatial coordinate.

• Minimum characteristic size (Lₘᵢₙ​ ): If we consider a system already bounded by the size

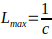
and apply the same logic to the internal structure, the minimum size at which a standing wave can still exist as a detached structure is

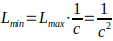
Hence, standing waves (particles) must exist in a range of characteristic sizes: .

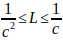
2. Mass limits (M):

Mass in this model is related to the energy of the transverse (electromagnetic in nature) component of the wave propagating along the sphere. Therefore, a 2π multiplier appears in the expressions for energy and mass, taking into account the geometry of the circle/sphere.

Energy Range (E): Similar to the dimensions, the energy will be in a range proportional to 2π/c² to 2π/c.

Mass range (M): Using E=Mc² (where M is the amplitude of the longitudinal wave associated with the mass of the particle), we obtain a range for M: M_{(min) (_) ₙᵤₘ=}(2π/c²ₙᵤₘ)/c²ₙᵤₘ=2π/c⁴ₙᵤₘ​ _{M(max) (_) ₙᵤₘ=}(2π/cₙᵤₘ)/c²ₙᵤₘ=2π/c³ₙᵤₘ. Thus, the amplitude of M (mass) is in the range:

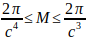
These ranges show that both size and mass are related to the speed of light in a stepwise manner. The ratio of the maximum and minimum values in each range (for L and for M) is cₙᵤₘ​ . This indicates that the quantisation of states inside these ranges should also follow the power law.

Here we see a value (constant) of 2π/c⁴, which is remarkably close to the value of Planck’s constant:

If:

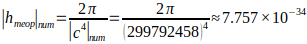
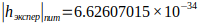
Then:

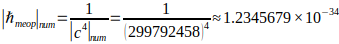
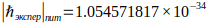
The difference from the experimentally obtained value of Planck’s constant is connected with that at calculation of the total mass of a standing wave, similarly to GR, it is necessary to take into account that gravitation «feels» the integral picture of density. If in the gaps between compactifications there is a void, then instead of just summation of masses it is necessary to take into account redistribution of work (energy) in space. This will be discussed below. This imposes its imprint on the value of the experimentally obtained Planck constant.

7.1.3 Node quantisation and elementary particle parameters

1. Condition for the formation of nodes:

For the formation of stable knots of a standing wave on a circle (representing the cross section of the spherical structure of the particle), the condition of consistency of the wave components is necessary. Let us assume that knots arise at equality of projections of interaction velocities on orthogonal x and y axes: υₓ​= υ_y.

• In polar coordinates, this condition means cosθ= sinθ, which is fulfilled at angles θ=π/4+nπ/2, where n∈ Z.
• On a complete circle (2π), this gives exactly four symmetric directions (45°, 135°, 225°, 315°) in which the formation of stable knots is possible. This leads to the assumption that no more than four basic stable standing wave types are possible, corresponding to 1, 2, 3, and 4 nodes.

Physically, this means that a standing node is formed only when the wave in its circular dynamics propagates energy uniformly along both spatial dimensions. If one of the velocity components becomes dominant (or equal to zero), either a purely translational wave (without nodes) or an unstable system incapable of stable self-consistent resonance arises.

The appearance of the fifth node breaks the equality of the velocity components, and the energy starts to go in the longitudinal direction — forming not a wave but a mass contribution.

2. Principle of degree quantisation:

Since the ranges for L and M are defined by degrees c, the division of these ranges into discrete levels (corresponding to n nodes) must also be degree-dependent. We have 4 types of stable wave states (particles). Conceptually, let us add to these 4 states a fifth «step» or «level» which, is associated with the «birth of mass» as an entity beyond the purely wave state, or with the transition to the next fractal level. Thus, the total number of conceptual «steps» or «divisions» for the full range of quantisation is accepted equal to five.

This 5-step quantisation assumption means that if we have some base multiplier K₀​ , then the nth level will be characterised by the multiplier (K₀)^n/5​ .

3. Definition of quantum of change and formulae for mass and wavelength:

• As a basis for scaling, let us take the quantity related to the ratio of the speed of light to the characteristic angular size 2π: K₀=cₙᵤₘ/(2π).
• Then the «quantisation multiplier» for the nth state will be (K₀​^)(1/5)or, for n n nodes, (K₀​^{)(n) (/5)}= (cₙᵤₘ​ /(2π)) ^{(n) (/5)}.

Based on the principle that the mass (M₀​ ) increases from its minimum Mₘᵢₙ_ₙᵤₘ​ , and the characteristic wavelength (λ₀​ ) decreases from its maximum characteristic value Lₘₐₓ_ₙᵤₘ 1/cₙᵤₘ​=​​ as the number of «quanta» n increases:

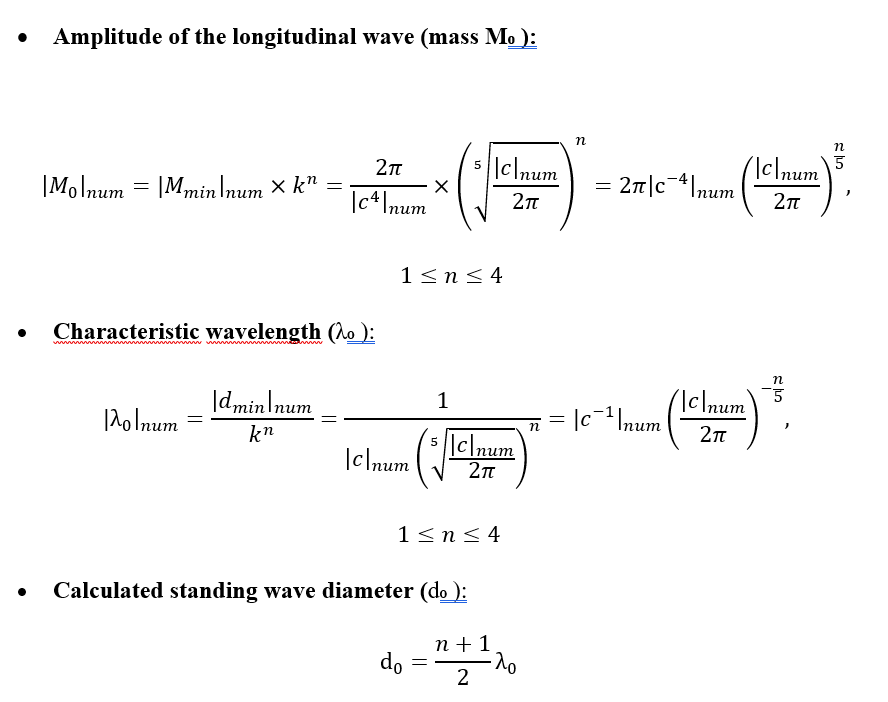
These formulas allow to relate the properties of particles (mass, size) to the number of nodes n of their wave structure, proceeding from the fundamental constant c and the principle of degree quantisation based on 5 conceptual levels.

Remark:
In this chapter, mass refers to the amplitude of a longitudinal wave. The total mass of a particle as a wave system consisting of several zones will be considered in the following chapters.

7.2 Extreme States of Wave Structures: From Photons to Limits of Energy Compression

In addition to the four primary types of stable standing waves corresponding to elementary particles with node numbers n=1,2,3,4, this model also considers limiting states characterised by n=0, n=−1, and n=5. These states do not describe stable massive particles but rather other forms of energy manifestation: electromagnetic waves, photons, and the ultimate compression of energy linked to fractal transitions.

7.2.1. States n=0 and n=−1: Photons and Electromagnetic Waves

States with n=0 and n=−1 within this model characterise electromagnetic radiation, particularly photons, and their transition to classical electromagnetic waves.

7.2.1.1. Limiting Wavelengths of the Photon

7.2.1.2. Mechanism of Photon Creation

A photon is created during dynamic processes involving changes in the energetic state of matter, for instance, when an electron transitions between energy levels in an atom. This transition is associated with the accelerated motion of the electron (a change in its wave structure).

• The accelerated motion of a charged electron constitutes a rapid, directed change in the energy density of the surrounding medium.
• This change generates a longitudinal wave of energy density, which, in turn, gives rise to its accompanying transverse electromagnetic component.
• Owing to the localisation and rapidity of the emission process, the forming electromagnetic wave does not have sufficient time to establish a fully closed spherical envelope. Instead, a wave structure is formed with an open, elongated envelope (in the direction of emission), resembling a paraboloid. This asymmetry (the ‘bulge’) dictates the directed motion of the photon.

7.2.1.3. Properties of the Photon

• Zero Rest Mass: The absence of a closed standing wave structure capable of retaining energy in a state of rest explains the photon’s zero rest mass.
• ‘Mass Equivalent’ and Directionality: The photon carries energy and momentum. The presence of a longitudinal wave component (albeit not a standing one in the sense of a massive particle) and the asymmetric form of its wave envelope (the non-coincidence of its geometric centre and ‘energy centre’ or ‘centre of mass’) are interconnected manifestations of its dynamic mass (E/c²) and ensure its directed motion.
• Spin: The structure of the photon’s boundary (envelope) may determine its spin properties, related to symmetry (or lack thereof) in the direction of motion, as well as possible ‘twisting’ of the wave along its propagation axis.

7.2.1.4. Transition to Classical Electromagnetic Waves

As the frequency of radiation decreases (wavelength increases, i.e., for n→−1 and beyond, past the λₘₐₓ photon​), the process of change in the source’s energetic state (e.g., in a radio antenna) becomes slower and more extended. The ‘bulge’ on the sphere of energy propagation becomes negligibly small compared to the overall sphere. Consequently, directionality is lost, and the radiation becomes predominantly spherical, corresponding to classical electromagnetic waves.

7.2.2. State n=5: Limit of Energy Compression and Fractal Transition

The state n=5 represents another extreme case within the model.

• Characteristics: It is proposed that at n=5, «all interaction velocity belongs to the energy domain.» This corresponds to the ultimate compression of energy.
• Size and Nature: Such a state is associated with the transition of energy into a region with a size less than |1/c²|ₙᵤₘ​ (the minimum size for particles with n=1..4). This region, existing within each elementary particle, is interpreted as an analogue of a black hole – a point of transition to a new, deeper level of spatial fractalisation (as per Postulate 5.1).
• Point-like Matter and Wave Functions: It is this region of ultimate energy compression (n=5) that can be considered a manifestation of ‘point-like matter’ (as per Postulate 5.2), whose behaviour within its surrounding wave field (the standing wave with n=1..4) may be described by wave functions, as is customary in quantum mechanics.
• Gravitational Waves: At n=5, the model predicts the phenomenon of energy compression and the possible emission of gravitational waves propagating in all directions. Appendix 9 also indicates that interaction with a macro-object at frequencies corresponding to n>4 can lead to energy transitioning into internal oscillations, manifesting as seismic activity or the generation of gravitational waves.

These extreme states (n=0,−1,5) extend the application of the wave model beyond the description of only stable massive particles, allowing for a qualitative interpretation of the nature of photons, electromagnetic waves, and possible mechanisms for fractal transitions at the sub-particle level.

Okay, here is the British English translation of the revised section 7.2.3, incorporating your points about the bullet-like shape and the offset centres of mass for gamma radiation:

7.2.3. High-Energy Quanta from Nuclear Interactions (Gamma Radiation)

A distinct type of high-energy electromagnetic radiation – gamma quanta – finds its explanation within this model not only through annihilation or the decay of elementary particles but also through more profound processes linked to the structural rearrangement of nucleons (protons and neutrons) themselves.

If nucleons are considered complex standing waves composed of several ‘semi-waves’ (as discussed in the context of their possible five-quark structure and the relation of charge to the work of a semi-wave), then during their intense interactions or rearrangements (e.g., in nuclear reactions), it is possible for individual such energetic fragments – ‘semi-wave shards’ – to be liberated.

These fragments are characterised by the following properties:

• They carry a significant portion of energy, determined by the invariant work associated with the formation of a semi-wave within the nucleon’s structure.
• Their characteristic dimensions (wavelengths) are commensurate with the sizes of nucleons (of the order of 10⁻¹⁵…10⁻¹⁶ m), which corresponds to their high energy (E=hc/λ).
• It is proposed that these ‘shards’, being dynamically liberated, acquire an asymmetric, elongated form, akin to a bullet. Such a formation leads to a non-coincidence of the geometric centre of this wave structure and its effective energy centre (or ‘physical centre of mass’). It is precisely this asymmetry and the uncompensated internal structure that compel this wave packet to move at the speed of light.
• Although such a fragment may represent a ‘closed’ portion of energy (e.g., one or several semi-waves from the original nucleon structure), it does not constitute a stable standing wave capable of existing at rest like a massive particle (i.e., it does not meet the conditions for n=1..4). Therefore, its energy must be radiated in the form of a moving gamma quantum.

Thus, gamma radiation is distinguished from photons in the optical or X-ray range (arising from electron transitions) not only by its considerably higher energy but also by the specific mechanism of its creation, being linked to the liberation and rearrangement of energetic sub-structures at the nucleon level. Their ‘bullet-like’ form and the resultant offset of centres explain their directed motion and corpuscular properties whilst retaining their wave nature.

7.3 Features of Elementary Particles in the Wave Model

In accordance with this model, the four primary stable types of elementary particles (neutrino, electron, neutron, and proton) represent standing waves with node numbers n=1,2,3, and 4 respectively. Each value of n defines unique geometrical and dynamic characteristics of the wave structure, which manifest as the specific properties of the particle.

7.3.1. Neutrino (n=1)

• Structure and Size: At n=1, a standing wave with a single node is formed. According to the formulae (from section 7.1.3), this state is characterised by the largest characteristic wavelength (λ₀​) and, consequently, the largest calculated diameter (d₀​) amongst the particles considered, commensurate with the size of an atom.
• Mass: It possesses the minimum wave amplitude (M₀​) and, as a result, the minimum mass.
• Interaction: Its large size and minimal mass render the neutrino a particle with very weak interaction with other matter.
• Internal Energy Rotation: The model posits that neutrino formation occurs when a portion of energy from the ‘spatial dimension’ is added to the ‘electromagnetic wave dimension’ (the transverse component propagating on a sphere). As the transverse EM wave is spherical in nature, this leads to the emergence of internal energy rotation within the neutrino’s structure. This distinguishes particles with an odd n (neutrino, neutron).
• Charge: The absence of charge is explained by the odd number of nodes and the presence of internal energy rotation, rather than a stationary boundary structure necessary for charge manifestation.

7.3.2. Electron (n=2)

• Structure and Charge: At n=2 (an even number of nodes), the particle receives a second portion of energy from the spatial side, which, according to the model, eliminates the internal energy rotation (characteristic of n=1) and leads to the appearance of electric charge.
• Nature of Charge: Charge is interpreted as the work performed by space (the energetic medium) to create one boundary semi-wave of the standing wave. The constancy of this work for all elementary wave units accounts for the quantisation and invariability of the elementary charge.
• Mass and Size: The wavelength λ₀​ and diameter d₀​ for the electron are smaller than those for the neutrino, whilst the amplitude M0​ (and, consequently, mass) is larger, according to the formulae in section 7.1.3.

7.3.3. Neutron (n=3)

• Structure and Internal Rotation: At n=3 (an odd number of nodes), a newly acquired portion of work (energy) again disrupts the symmetry required for charge, reinstating the effect of internal energy rotation within the particle, analogously to the neutrino.
• Charge: It is an electrically neutral particle.
• Mass and Size: Compared to the electron, the neutron has a smaller λ₀​ and d₀​, and a larger M₀​ (base amplitude/mass). However, as will be detailed in section 7.7.5, its observed mass requires additional factors to be considered. It is important to note that standard physics typically does not consider such internal energy rotation as a direct additive contribution to the rest mass of neutral particles in this manner. In this model, however, it is proposed that this rotational energy, during the neutron’s interactions (e.g., when its mass is determined via decay products or in nuclear interactions), may manifest as an additional contribution to its effective, measured mass. This is analogous to how, if the observed electrostatic interaction force between charged particles were mistakenly interpreted not as a manifestation of their charges but as an additional contribution to their individual masses, it would also lead to an overestimation of the latter. Thus, in your model, the ‘geometric’ mass of the neutron, determined solely by the standing wave amplitude M₀​ for n=3, might be lower than that of the proton (n=4), but its experimentally determined mass appears higher precisely due to this (unaccounted for in standard models, or differently interpreted) contribution from internal energy rotation.
• Quantum Entanglement: Like other particles with an odd n and internal energy rotation, neutrons (when pair-produced with antineutrons) exist in a state of quantum entanglement. This property, as previously discussed, can influence their stability and decay characteristics.

7.3.4. Proton (n=4)

• Structure and Charge: At n=4 (an even number of nodes), the situation is analogous to the electron: the structure again becomes such that internal energy rotation is absent, and the particle exhibits electric charge.
• Sign of Charge: The model posits that for the proton, the sign of the charge will be opposite to that of the electron’s charge. This may be related to a different configuration or ‘direction’ of the work performed by space in forming the boundary semi-wave for n=2 and n=4.
• Mass and Size: The proton possesses the smallest λ₀​ and d₀​, and the largest M₀​ (mass) among the four particles considered.

7.3.5. General Principle: Energy Rotation or Charge

The model leads to the conclusion that for the principal stable particles, there is a form of alternative: «either we have internal energy rotation (for odd n), or charge (for even n).» This reflects two distinct ways in which a particle’s wave structure can interact with the surrounding energetic medium or manifest its internal dynamics.

7.3.6. Pair Production of Particles

It is important to note that, in accordance with the law of conservation of energy, the creation of particles (as wave structures from the energy of the medium) should occur in pairs (particle-antiparticle). For neutral particles, such as neutron-antineutron or neutrino-antineutrino, the distinction within a pair may lie in the opposing directions of internal energy rotation, which conditions their quantum entanglement.

This description of the features of elementary particles arises from their representation as standing waves with varying numbers of nodes, which determines their key physical characteristics within the proposed theory.

7.4 The Nature of Elementary Particles in the Wave Model

The representation of elementary particles as standing waves not only allows for the calculation of their parameters but also offers intuitive images of their structure and interactions, explaining their key properties.

7.4.1. Idealised Model: Spherical Wave with Internal Structure

In its simplest, idealised representation, an elementary particle (a standing wave, as per Postulate 2.1) can be likened to a spherical object. Within this sphere, regions of increased and decreased energy density alternate, forming an internal structure of semi-waves. This picture resembles a resilient ball undergoing complex volumetric oscillations.

• For neutral particles (with an odd n, such as neutrinos and neutrons), in addition to the radial distribution of energy density, the presence of internal rotation or ‘torsion’ of energy density along a certain axis is characteristic. This is a consequence of their specific wave configuration, as discussed in section 7.3.

7.4.2. The Real Particle: Interaction with the Medium, Spin, and Forces

In practice, the ideal spherical form of a particle is inevitably distorted.

• The process of particle creation (as a wave formation from the energy of the medium) is accompanied by changes in energy density in the surrounding space.
• As a particle has a finite size, its boundary is acted upon by forces of varying magnitude and direction from the energetic medium (as per Postulate 1.2), which leads to the distortion of its wave envelope.
• It is this dynamic distortion and asymmetry of the real wave structure of a particle, arising from its interaction with the medium, that is proposed in this model as the mechanism for the origin of spin. Spin, therefore, is not an initially inherent abstract property but reflects the geometry and dynamics of a real wave object.
• The asymmetry of form and energy distribution also leads to the emergence of interaction forces between particles.

7.4.3. Manifestation of the Work of Space: Charge and Internal Rotation

A fundamental principle, following from the unity of space and the resonant character of all interactions (as per Postulates 1.2 and 3.1), is the invariance of the work performed by space (the energetic medium) in forming each semi-wave of a particle’s standing wave. This work manifests differently for charged and neutral particles:

• Charged particles (n is even, such as electrons and protons): The work of space is realised in the formation of a stable gradient of energy density at the particle’s boundary – either an increased or decreased density compared to the medium. This gradient is the manifestation of electric charge. The charge is related to the work expended in creating one boundary semi-wave. The constancy (quantisation) of the elementary charge is a direct consequence of the invariance of this work.
• Neutral particles (n is odd, such as neutrinos and neutrons): For these particles, the work of space manifests not as an external density gradient but as the organisation of internal energy rotation (or ‘torsion’ of energy density). This is also a characteristic of the work expended by space to maintain their specific wave structure.

7.4.4. Particle Mass: A Dynamic Characteristic and the Influence of Internal Rotation

• Mass as Amplitude: In this model, the mass M₀​ of a particle (as per Postulate 2.3.1) is directly related to the amplitude of its longitudinal standing wave.
• Conservation of Work during Motion: When the velocity of a particle changes, its wave structure (size, wavelength λ₀​) alters. For the invariant work (W=M₀​λ₀​/π) per semi-wave to be conserved, the amplitude M₀​ (i.e., mass) must also change. This explains the relativistic change in mass with changes in velocity and size.
• Influence of Internal Rotation on the Measured Mass of Neutral Particles: The energy of internal rotation, inherent to neutral particles (neutrinos, neutrons), contributes significantly to their measured mass. Standard methods of mass determination… record the total energy of the particle without distinguishing between the contribution from the ‘pure’ amplitude of the standing wave and the contribution from the energy of its internal rotation.
  • This ‘additional’ manifestation of rotational energy can be complex. Analogous to a magnetic dipole, the internal rotation of energy may create a form of ‘poles’. When interacting with charged particles or external fields, it might manifest uniformly (e.g., as an effective attraction, adding to the gravitational one). However, when two such neutral particles interact with each other, their ‘rotational moments’ could interact in a manner similar to magnets, leading to both attraction and repulsion depending on their mutual orientation.
  • In experiments determining mass, where various orientations and types of interactions are averaged, this rotational effect may yield an averaged, ‘uniform’ contribution to the measured effective mass.
  • Whilst the effects of charge are accounted for when determining the mass of charged particles… a similar consideration for the ‘energy of rotation’ in neutral particles is not standardly made.
  • It is precisely this unaccounted for (or differently interpreted) contribution from internal energy rotation, that leads to the experimentally measured mass of the neutron being higher than might be expected from a simple comparison of node numbers (n=3 for the neutron versus n=4 for the proton), if only the ‘geometric’ mass from the standing wave amplitude were considered. This explains the necessity of introducing correction factors when calculating the masses of neutral particles within this model (see section 7.7.5).

Thus, elementary particles in this model are presented as complex, dynamic wave structures, whose observable properties (mass, charge, spin) are manifestations of their geometry, internal energy dynamics, and interaction with the surrounding energetic medium.

7.5 Interference of Standing Waves (Particles)

7.5.1. Principles of Interaction of Standing Waves (Particles) in this Model

As previously established, elementary particles in this model represent stable standing waves (as per Postulate 2.1), whose internal structure is formed in such a way as to maximally utilise the available interaction speed (c) within the energetic medium (as per Postulate 1.2). This implies that each particle is a densely packed, resonant wave formation.

Direct ‘penetration’ of one such standing wave (particle) into another without disrupting their internal structures appears impossible. This is corroborated by experimental observations, for example, in nuclear reactions, where significant energies, leading to a complete rearrangement of their wave structures, are required for the fusion or fission of particles.

Instead of mechanical penetration, interaction between particles in this model occurs through an exchange of energy, conditioned by the ‘work of space’. The ‘work of space’ is understood as the energy expended or released by the energetic medium during the formation or alteration of the particles’ wave structures (see section 7.6 concerning the nature of charge). The system strives to minimise the overall energetic stress (or total work of space):

• Oppositely charged particles attract because their combined field formation requires less total work of space compared to their separate existence.
• Like-charged particles repel because their proximity increases the overall stress and necessitates greater work of space.
• Uncharged rotating particles (e.g., neutrons) may also exhibit mutual attraction (strong interaction at short distances) due to the interaction of their ‘energetic moments’ or fields created by the internal rotation of energy, which is also linked to the minimisation of the work of space in a specific configuration.

These mechanisms describe the direct force interactions of particles. The phenomenon of interference, however, arises under different conditions, when these direct interactions are weakened, and other aspects of the wave nature of particles and their interaction with the medium come to the fore.

7.5.2. Conditions for the Emergence of Interference: Weakening of Direct Interaction

Interference is typically observed when particles pass through narrow slits, diffraction gratings, or are reflected from thin films. In such situations, direct ‘force’ interaction between particles (if their flux is sufficiently rarefied) or between a particle and the massive parts of the experimental setup (excluding the edges of obstacles) is minimised.

• The Single-Slit Experiment as an Example: When a particle (wave) passes through a single slit, it interacts predominantly with the edges of this slit. If the slit is sufficiently narrow (commensurate with the particle’s wavelength), its wave structure undergoes diffractive distortion. In this model, this can be interpreted as the ‘work of space’ at the slit edges altering the configuration of the passing wave. In this state, the wave is no longer entirely a standing wave in the sense of a free particle but is rather a perturbation propagating with minimal ‘resistance’ from the medium after traversing the slit.

7.5.3. Interference as a Resonance of the Wave Structure with the Medium Modulated by Obstacles

The classical explanation of interference (e.g., in Young’s double-slit experiment) is based on the principle of wave superposition. Within this model, this phenomenon can be further elucidated by considering it as the result of a resonant interaction of each individual particle’s wave structure with the energetic medium, whose properties are locally modulated by the presence of obstacles (slits).

• Slits as Modulators of the Medium: Two (or more) slits create specific boundary conditions for the ‘work of space’ and the propagation of wave disturbances in the medium. They act as secondary coherent sources or as channels through which the particle’s wave structure can pass, undergoing certain phase changes.
• Resonant Propagation: Each particle (wave), upon passing through the system of slits, interacts with this modulated medium. Its subsequent propagation is not arbitrary but is directed along trajectories corresponding to constructive resonance with its own wave structure and the structure of the medium as altered by the slits. That is, the particle predominantly arrives in those regions of the screen where the conditions for its wave propagation (considering the phase shifts introduced by the slits) are resonantly ‘permitted’ or energetically favourable.
• Formation of the Interference Pattern: The totality of such resonant trajectories for a multitude of particles forms the observed interference pattern of alternating maxima and minima.

7.5.4. Connection with the Wave Function and Probabilistic Description in Quantum Mechanics

Standard quantum mechanics describes the interference of single particles via a wave function, the square of whose modulus determines the probability of detecting the particle at a particular point. In this model, this probabilistic description may receive the following interpretation:

• The wave function in quantum mechanics can be regarded as a mathematical tool effectively describing the resultant distribution of possible resonant paths for the particle-wave under the given experimental conditions.
• Regions of high probability (interference maxima) correspond to zones where conditions for constructive resonance of the particle’s wave structure with the medium (modulated by the slits) are most favourable.
• Regions of low probability (minima) are zones where resonant conditions are not met or lead to destructive superposition of wave components.

Thus, interference in this model is not merely an abstract superposition of waves but a consequence of specific resonant conditions arising from the interaction of a particle’s wave structure with an energetic medium whose properties are altered by the presence of obstacles. This approach aims to provide a more physical picture of the phenomenon, without contradicting the successful mathematical apparatus of quantum mechanics.

7.6 Work as the Basis of Charge: A Geometrical Interpretation

In the preceding sections, it was demonstrated that elementary particles, in this model, are standing waves in space (as per Postulate 2.1), formed under the influence of the energy of the medium (as per Postulates 1.1 and 1.2). Space (the energetic medium) performs work in creating an oscillatory structure – a standing wave with a specific number of nodes. This work, in each elementary portion of the wave, is expressed in the form of a semi-wave. The question arises: what is the precise physical meaning of the work performed in this process, and how does it relate to a fundamental characteristic of a particle – its electric charge?

7.6.1. The Geometrical Nature of the Invariant Work of a Semi-Wave

Let us represent an elementary particle as a standing wave composed of n+1 semi-waves (according to section 7.1.3). Each semi-wave is a sinusoidal oscillation of energy density, arising from the energetic interaction of space with a local region. If we assume the oscillation profile to be sinusoidal, the area under one semi-wave (which in this model is interpreted as the work W performed by space to create this semi-wave) can be defined as:

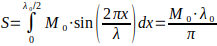
where:

• M₀​ is the amplitude of the wave, corresponding in our model to the ‘amplitude mass’;
• λ₀​ is the characteristic wavelength (the size of one complete oscillation).

Thus, the work per semi-wave is:

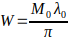
Substituting into this equation the formulae for calculating the amplitude M0​ and wavelength λ0​ from section 7.1.3:

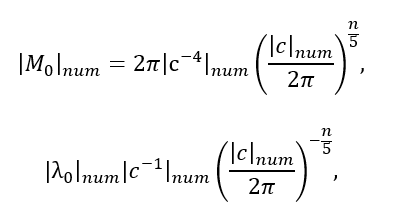
From the final expression, it is evident that the work W, performed by space to create one semi-wave, is an invariant quantity, independent of the number of nodes n of the standing wave. This is a key consequence of the model, as the formulae for M₀​ and λ₀​ were initially constructed based on the principle of conserving this work.

7.6.2. From Invariant Work to Physical Charge: The Role of Symmetry and the Fine-Structure Constant

As charge in this model is understood as a fundamental characteristic determining a particle’s interaction with an electromagnetic field, and interaction is a result of energetic work (as per Postulates 3.1 and 3.2), it is logical to associate charge with this invariant work W.

It is proposed that the boundary semi-wave of the particle is responsible for its direct electromagnetic interaction with an external field – it is this that creates effects at distances exceeding the particle’s own size. However, the work W itself characterises the energetic contribution to the structure of the semi-wave. For this work to manifest as an interaction force in external space, the scale of this manifestation must be considered.

However, it should be considered that this quantity, 12/π|c²|ₙᵤₘ​, characterises the total work density associated with the formation of the particle as a stable wave structure under the influence of a symmetrical, omnidirectional ‘pressure’ from the energetic medium. In this model, the particle is viewed as a local condensation of energy around a centre of mass, which is situated in the middle of the volumetric wave construct. Space acts symmetrically upon this construct from all directions to maintain it.

During the external interaction of two such particles at sufficiently large distances (e.g., in Coulomb’s law), where we can consider them as point-like centres of force, the interaction along a specific direction will be determined not by the entire spherical work of formation, but rather by its effective ‘projection’ or ‘half-contribution’ relative to the line connecting their centres of mass. One might say that, owing to the symmetry of the ‘particle-medium’ system, only the component of the ‘work of space’ pertaining to ‘half’ of the complete spherical structure, oriented in the given direction, comes into effect during an interaction along a specific direction. That is, the total work W (or its density) is distributed around the centre of mass in all directions, but in a pairwise interaction at a distance, two principal ‘directions’ of action along the line connecting them can be distinguished.

Consequently, the effective amount of work participating in external electromagnetic interaction (let us term it the ‘effective geometrical charge’, q_{eff_geom}​) participating in an external electromagnetic interaction along a specific direction will be half of the total work density calculated for the entire spherical structure:

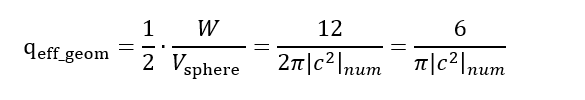
Numerically, q_{eff_geom}​≈2.12518×10⁻¹⁷ (in arbitrary units, where cₙᵤₘ​ is the numerical value of the speed of light).

• Introduction of the Fine-Structure Constant (α) and Physical Charge (e): This value q_{eff_geom​} is comparable to the elementary charge e≈1.602×10⁻¹⁹ C via the fine-structure constant α≈1/137.036:

e≈q_{eff_geom​}⋅α

More precisely, q_{phys_calc​}=q_{eff_geom​}⋅α≈(2.12518×10⁻¹⁷)/137.036≈1.5508×10⁻¹⁹ (in arbitrary units of charge, if α is dimensionless). This value is close to the experimental elementary charge, as noted in section 4.

• Interpretation of α: The fine-structure constant α, in this model, acts not as a primary constant of the electromagnetic interaction strength, but as a coefficient of the efficiency of manifestation of this geometrical work in external space. It reflects what fraction of the ‘raw’ geometrical work of a semi-wave actually participates in external electromagnetic interactions. The smallness of α implies that only a minor portion of this structural work is effectively ‘radiated’ or manifested outwardly. This efficiency may depend on the properties of the energetic medium itself (its ‘permeability’ to this type of work, or ‘viscosity’), which, in turn, could be related to the local energy density and, consequently, to the gravitational potential.
• Constancy of the Elementary Charge e: This is explained by the invariance of the work W required to create a semi-wave and, under terrestrial conditions, the observed constancy of α. If α indeed depends on the gravitational potential, then under different conditions e could possess a different value (which is testable via the experiment proposed in section 7.6.4). This also explains why charge does not depend on the number of nodes (apart from the condition of evenness for its emergence) or the particle’s velocity – it reflects the fundamental act of space performing work to create a stable wave unit capable of external electromagnetic interaction.

7.6.3 On the nature of the fine structure constant

It has been shown above that the value of the elementary charge calculated from geometrical relations differs from the experimentally measured one — and this difference is a multiple of the fine structure constant. Moreover, it is important that the experimental value of the charge is smaller than the theoretical one.

What can this mean? First of all, it should be noted that the values of the elementary charge and fine structure constant used in modern physics were obtained near the Earth’s surface. In space they are considered to be universal constants. There were attempts to indirectly determine the fine structure constant on the scale of the Universe, but they did not lead to an unambiguous confirmation of its variability and were not widely recognised. In most models these quantities are considered unchanged.

If we consider this question from the position of the wave model of matter, a different explanation becomes possible. The process of «reduction» of the geometrical charge value can be interpreted as a result of the influence of the surrounding gravitational field created by the macro-object. This field forms a local compaction of the energy medium, similar to «viscosity», in which the wave interaction takes place. In such a medium, the efficiency of interaction between clots of energy is reduced — similar to the way metal balls in honey collide with less energy than in air.

Within the framework of the proposed model, we can give a new interpretation of the nature of the fine structure constantα. This value acts not as an arbitrary numerical constant, but as a coefficient reflecting the local influence of the energy density of space determined by the mass of the surrounding macroobject (e.g., a planet). Thus,αmay not be a universal but a context-dependent quantity determined by geometry and background density.

Such assumption admits experimental verification: for example, by determination of the elementary charge orαat different altitudes above sea level, in conditions of reduced gravitational density. The appearance of statistically significant deviations will be an indirect confirmation of the proposed model.

7.6.4 A Possible Experiment to Test the Variability of the Fine-Structure Constant

The proposed model allows for a simple experimental test that does not require precise measurement of the elementary charge but can still reveal a possible variation in the strength of electrostatic interaction under different conditions. The goal of the experiment is to detect whether the fine-structure constant α may vary depending on gravitational conditions.

The following experimental setup can be used:

Two identical metallic spheres are mounted in a horizontal plane and attached to symmetric elastic elements—such as light springs or stretched nylon threads. The spheres are free to move in the horizontal plane under electrostatic repulsion. Each sphere is connected to a common charge source, ensuring equal distribution of electric charge. Vertical gravitational force does not influence the interaction between the spheres, as their motion is restricted to the horizontal axis.

Once the system is charged, the spheres begin to repel each other, stretching the elastic elements until equilibrium is reached—where the repulsive force is balanced by the restoring force of the springs. The equilibrium distance between the spheres (denoted as r) depends on the square of the charge, since the Coulomb force is proportional to q². With fixed spring stiffness and constant external charge, any change in r under different gravitational conditions (e.g., at various altitudes or in microgravity) may indicate a change in the effective value of the charge—and hence a possible variation in the fine-structure constant α.

As was aptly noted in a comment on Habr:

«The elastic forces in the spring material are also electromagnetic in nature—not between the spheres, but between the electron shells of atoms. The fine-structure constant affects them just as it affects the interaction between the spheres.»…

However, there is an important nuance: the states of electron shells in atoms are in resonant interaction with the surrounding gravitational field. This implies that a change in the gravitational environment may lead to a corresponding resonant change in the material’s density, thus affecting the elasticity. For the spheres themselves, such a resonant effect (affecting the initial separation) is not expected. If the fine-structure constant indeed plays the role of a kind of «gravitational viscosity» of space, then the resulting imbalance between elastic and electrostatic forces may qualitatively indicate that α is not a true constant but varies depending on the gravitational environment.

Thus, even without direct measurement of the elementary charge, the experiment can detect a possible influence of gravitational density on electrostatic interaction. This would serve as an indirect but significant confirmation of the model proposed in this work.

7.7 The Nature of Mass and the Calculation of its Values via Longitudinal Wave Amplitudes

In this model, mass is not an initially inherent property of matter but arises as a dynamic characteristic of stable wave processes – standing waves formed within an energy-saturated medium (as per Postulates 1.2 and 2.1). The mass of a particle is directly related to the amplitude (M₀​​) of its longitudinal standing wave and the specifics of its internal structure. The ‘perception’ or manifestation of this mass occurs at the centre of the wave structure – its centre of mass, which in this model is considered a ‘point’ devoid of its own size.

7.7.1. Mass as a Manifestation of Local Energy Condensation and the Invariance of Work

As established in section 7.1.3, the base amplitude of the longitudinal wave M₀​​ for a particle with n nodes is determined by the formula:

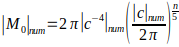
This amplitude reflects the local condensation of energy in the particle’s region. A fundamental principle is the invariance of the work W=M₀​λ₀​/π=2|c⁻⁵|ₙᵤₘ​ performed by space to create each semi-wave (section 7.6.1). When conditions change (e.g., when a particle moves), its wave structure (size λ₀​​) alters, leading to a corresponding change in the amplitude M₀​​ to preserve the invariance of W. This explains the relativistic change in mass.

7.7.2. Calculation of Electron Mass (n=2)

The electron, having two nodes (n=2), is a charged particle with a comparatively simple structure. Its mass is considered to be formed by one primary central region of energy condensation.

• Base Mass: The amplitude of this central region, M₀​ (for n=2), constitutes its base mass.
• Symmetry Principle and Mass Manifestation: As this mass is already localised at the centre (the ‘point’ of the centre of mass) and lacks symmetrical ‘arms’ influencing external interaction in the same way as distributed charge, the ‘half-contribution due to symmetry’ principle (discussed for distributed charge) is not applied here. The central mass manifests fully in interactions.
• Resultant Electron Mass: m_e​=M₀​ (for n=2) Using |M₀|ₙᵤₘ​≈9.144×10⁻³¹ kg (from Appendix 7), this value aligns well with the experimental mass of the electron (9.109×10⁻³¹ kg), supporting this approach for the electron (see table in section 4).

7.7.3. Calculation of Proton Mass (n=4)

The proton (n=4) possesses a more complex structure, involving both central and peripheral regions of increased energy density.

• Central Semi-wave: This contributes to the base mass an amount equal to M₀​ (where M₀​ is calculated for n=4). This central component, akin to that of the electron, is not halved due to the symmetry of external manifestation, as it itself constitutes the centre of symmetry.
• Peripheral Semi-waves (‘Arms’): The proton also has two symmetrical peripheral regions of increased density, which are separated from the centre by regions of decreased density (‘voids’). To account for the contribution of these peripheral structures to the total mass, the following principle of averaging and conservation of invariant work is adopted in this model: the ‘voids’ preceding these peripheral regions are conceptually eliminated, and the peripheral semi-waves themselves are, as it were, ‘stretched’ to occupy the vacated space. To ensure that the invariant work (W=M₀​λ₀​/π) for them is conserved during such an increase in their effective length, their amplitude must decrease. If it is assumed that their effective length is doubled, then the amplitude of each is halved. Thus, each of the two peripheral ‘arms’ contributes an effective amplitude of M₀​/2.
• Total Contribution of Peripheral ‘Arms’ and Symmetry of External Manifestation: The combined structural contribution from these two peripheral ‘arms’ is M₀​/2+M₀​/2=M₀​. It is to this total contribution from the peripheral arms that the ‘half-contribution due to symmetry’ principle is applied during external interaction along a specific direction (as discussed for charge in section 7.6.2). That is, the effective contribution from both arms to external interactions will be M₀​/2.
• Resultant Proton Mass: Summing the contribution from the central part and the effective contribution from the peripheral arms, we obtain:

m_proton​=M₀​(centre)+M₀/2(effective contribution from arms)=(3/2)M₀​

(where M₀​ is the base amplitude for n=4). Using |M₀|ₙᵤₘ​ ​ for n=4≈1.07797×10⁻²⁷ kg (Appendix 7), we get mproton​≈1.61695×10⁻²⁷ kg, which is very close to the experimental value and explains the 3/2 factor.

7.7.4. Calculation of Neutron Mass (n=3) – A Revised Approach

The neutron (n=3), being a particle with an odd number of nodes, possesses internal energy rotation, a key feature that significantly influences its observed mass. Its structure is asymmetric compared to the proton.

• Structural Mass (excluding direct rotational contribution): Let us assume the neutron’s asymmetric structure forms effective ‘arms’ relative to its centre of mass as follows: from one side, a wave structure contributes an effective amplitude M₀​ (where M₀​ is the base amplitude for n=3), and from the other side, a structure contributes an effective amplitude M₀​/2 (after a correction for ‘voids’ similar to the proton’s for this part of the structure). The total structural contribution from these asymmetric arms would be M₀​+M₀​/2=(3/2)M₀​. The neutron’s internal rotation, it is proposed, imparts an effective ‘point-like’ nature or symmetrises it for the external manifestation of this structural mass. Therefore, unlike the charge or non-rotating symmetric structures, an additional halving due to symmetry of external manifestation is not applied to this (3/2)M₀​ quantity. Thus, the ‘purely structural’ mass of the neutron, if it were not to possess additional rotational energy, would manifest as (3/2)M₀​. Numerically:

(3/2)⋅M₀​(for n=3)≈(3/2)⋅(3.142×10⁻²⁹ kg)≈4.713×10⁻²⁹ kg.

• Contribution of Rotational Energy to Mass: The energy of this internal rotation (Erot​) provides the dominant contribution to the observed mass. To ‘activate’ or fully manifest this structural mass (3/2)M₀ as a particle with rotation, it must be ‘spun up’. This ‘work of spinning up’ or rotational energy significantly increases the effective mass. In this model, it is proposed that this transition from a non-rotating structural mass to the observed mass of the rotating neutron is described by multiplication with the coefficient k≈34.3343 (previously introduced as the ‘minimum quantum of change’ or a scaling factor related to k=(cₙᵤₘ​/(2π)) ^1/5:

m_neutron​=(3/2)M₀⋅k

m_neutron​≈(4.713×10⁻²⁹ kg)⋅34.3343≈1.61817×10⁻²⁷ kg.

This value agrees well with the experimental mass of the neutron.

7.7.5 Specifics of Neutrino Mass (n=1)

The case of neutrinos deserves special attention. According to the proposed wave model, the mass cannot be less than a certain lower limit due to the fundamental quantity 2π/c⁴. The neutrino possesses at least one half-wave, which can be interpreted as a contribution to the mass. Even ignoring the energy spin within the neutrino, this gives a minimum mass estimate of 2,664×10⁻³²kg. However, experimental estimates of the neutrino mass are much lower, up to 8,6×10⁻³⁷ kg. This discrepancy in experience is due to the fact that the neutrino has a significantly longer wavelength than other particles (about 10⁻¹¹ m versus 10⁻¹⁵ m for the proton). Since mass is associated with a specific point, matter, and β-decay always involves more massive particles like the proton or neutron, they are the ones that set the scale of measurement. Their wavelength determines the scale to which the neutrino is «bound» in the measurement. As a result, the mass associated with the wave structure of the neutrino is «smeared» on a much larger scale, and the perceived value decreases in proportion to the increase in scale:

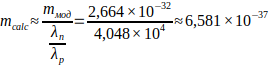
which is within the experimental constraints. Thus, the proposed model does not contradict the observed data and explains why the neutrino mass appears to be so small: it reflects the energy amplitude distributed in the external space. This confirms the idea that the mass is not a fundamental quantity, but a consequence of the geometry of the wave configuration and its local concentration.

7.7.6 Antimatter and antigravity

For antimatter the structure is opposite: In the centre of the particle a region with reduced energy density is formed, which leads not to attraction but to repulsion, to antigravity.

• In matter: centre attracts → mass is positive.
• In antimatter: the centre repels → mass manifests as «negative» gravity.

This explains the natural «scattering» of antimatter and its rarity in the observable Universe.

7.7.7 Measuring galaxy masses

In the case of galaxies, mass measurements are not direct either. Mass is determined from the rotational velocities of stars in the periphery and from the gravitational effects on surrounding objects. These methods automatically include the effects created by the dynamic structure of the galaxy itself, including internal flows and vortices. Thus, the mass estimate includes not only the «real» mass of matter, but also the gravitational equivalent of the rotational energy — similar to the neutron.

In this regard, when scaling from neutron to galaxy size (Appendix 8, the calculation is based on the formulas of the next chapter «7.10 Fractality of the Universe structure.»), it is necessary to use the corrected mass, taking into account the effect of internal rotation, to obtain a correspondence with the observed characteristics.

7.7.8 Why is the contribution of lower density zones not taken into account?

Gravity responds to positive energy density. That is: gravitational attraction is created where energy is concentrated, not where it is «rarefied».

Although the phenomenon of antigravity for antiparticles has not yet been detected in experience, but from this paper it follows as an obligatory element, so similarly to the previous paragraph we can conclude the following:

Antigravity responds to negative energy density. That is: antigravity repulsion is created where energy is discharged, not where it is «concentrated»

In the equations of the general theory of relativity (GTR), mass is part of the energy-momentum tensor:

Tμν

And the gravitational field is defined where Tμν​ is positive, that is, where there is positive energy. Sparse areas where the energy density is less — they don’t create «negative mass», they just reduce the average density.

In other words:

• Density increase → active contribution to mass.
• Density reduction → passive influence: stretches density zones, affects «average mass» but does not create negative mass.

Reduced density does not «subtract» mass because:

• Gravity arises from the presence of energy densification, not rarefaction.
• The void only increases the «smearing» of the mass, making it more distributed, but does not destroy the densification itself in density zones.

In other words, the lower density zones do not add negative mass, they only reduce the average mass density in space. It is the redistribution that leads to the need to correct the amplitude in the calculations.

7.8 Fractality of the Structure of the Universe

One of the fundamental principles embedded in this model is the fractality of the structure of matter and the Universe (as per Postulate 5.1). This principle implies self-similarity in wave formations and physical laws at various scales, from the microcosm of elementary particles to cosmological structures.

7.8.1. Preconditions for Fractality: Limits of Dimensions and Energy Quantisation

As has been shown in section 7.1.2, natural limits exist for the dimensions (1/|c²|ₙᵤₘ≲L≲1/|c|ₙᵤₘ) and masses (2π/|c⁴|ₙᵤₘ≲M≲2π/|c³|ₙᵤₘ​​) of stable standing waves at our observable level. When these limits are exceeded, the interaction speed c is no longer capable of sustaining wave processes with the same parameters, which necessitates a step-like transition to a different fractal level. The quantity 2π/|c⁴|ₙᵤₘ​, corresponding to the minimum mass of a standing wave, plays a key role in this transition. It is the theoretical analogue of Planck’s constant h and provides the basis for quantisation and scaling.

7.8.2. Formula for Fractal Energy Scaling and its Components

To describe the transition between fractal levels, the concept of a level n is introduced (n∈Z, where n=0 corresponds to our world). The energy of a system at any level n is expressed through its mass Mn​ and characteristic interaction speed Cₙ​ as Eₙ​=Mₙ​Cₙ²​. In this model, it is proposed that the total energy associated with a base mass m and the speed of light c at level n=0 remains invariant upon scaling: Eₙ​=Mₙ​Cₙ²​​. This is achieved through the congruent scaling of Mₙ​ and Cₙ​ via a fundamental ‘scaling quantum’.

• Principle of Separating Geometry and Physics: The theoretical Planck’s constant in our model is h_{theor_num​}=2π/|c⁴|ₙᵤₘ​. This expression can be separated into two parts: 2π – a dimensionless multiplier reflecting the universal circular/spherical geometry of wave processes , and 1/c⁴ – a quantity dependent only on c, the fundamental constant defining the physics of our world.
• Choice of Scaling Quantum: It is logical to assume that the quantum defining transitions between levels of our fractal series should be related to the physics of our world (c), rather than the universal geometry (2π). Therefore, it is more correct to use the reduced Planck’s constant, which is cleansed of the geometric multiplier 2π, as the scaling quantum. We denote its theoretical analogue ℏ_quant​: ℏ_quant_ₙᵤₘ​=h_theor_ₙᵤₘ​/(2π)=(2π/|c⁴|ₙᵤₘ​)/(2π)=1/|c⁴|ₙᵤₘ

Now, using ℏ_quant ​ as the basis, we can write the scaling laws:

• Relative mass at level n (Mₙ​): Mₙ​=m⋅(ℏ_{quant_num}​)²ⁿ= m⋅(1/|c⁴|ₙᵤₘ​)²ⁿ
• Relative interaction speed at level n (Cₙ​): Cₙ=c/(ℏ_{quant_num})ⁿ=c⋅(|c⁴|ₙᵤₘ​)ⁿ

Substituting these expressions into Eₙ​=Mₙ​Cₙ²​ ​ confirms the invariance of energy, Eₙ​=mc².

7.8.3. Interpretation of the Speed of Light and Planck’s Constant in the Fractal Model

• Speed of Light: The quantity c is the fundamental constant of our level, n=0. The quantity Cn​ is the effective interaction speed at level n, as it would be perceived from our level. For a hypothetical observer within level n, their own limiting speed would be for them the same constant as c is for us. When transitioning from one fractal level to another, the laws of physics and local fundamental constants do not change.
• Planck’s Constant: Planck’s constant (h and ℏ) is not independent but emerges as a consequence of the structure of wave interaction, defined through c and geometry (2π). Its experimental value, h_exp​, may differ from the theoretical h_theor​=2π/c⁴ because it is measured using complex nucleons, which introduce a ‘structural distortion’ into the system of measurements (as discussed in Appendix 7.5).

7.8.4. The Scaling Law for Size

In section 7.1.2, we established the maximum limiting size of a standing wave at our interaction speed c:

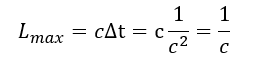
Accordingly:

• At the base level (n=0): L₀​=1/c
• At level n: Lₙ​=1/Cₙ

Given that Cₙ=c/(ℏ_quant_ₙᵤₘ)ⁿ=c⋅(|c⁴|ₙᵤₘ​)ⁿ=с(ℏ_quant_ₙᵤₘ)⁻ⁿ, we can find the ratio: L₀/Lₙ=(1/c)/(1/Cₙ)= Cₙ/c=(ℏ_quant_ₙᵤₘ)⁻ⁿ From this, we find the formula for size:

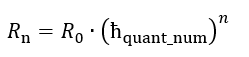
With this approach, the Universe acquires a potentially infinite fractal structure where the variable n has no strict limitations. Quantisation is expressed in the step-wise change of the relative speed of light Cₙ​​, which automatically defines the scale transitions and their corresponding energy densities.

The key conclusion from the principle of fractal scaling is the resultant relationship for the energy of a structure at any given fractality level n. Based on the premises of the fractal nature of matter and the scaling of its primary physical characteristics, the energy Eₙ​​ is expressed as follows:

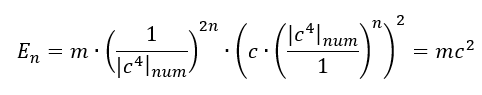
This result demonstrates the fundamental conservation (invariance) of energy during transitions between fractal levels in the proposed model of the Universe. The practical application of this principle is examined in detail in Appendix 8.

7.8.5. The Scaling Law for Frequency and the Nature of Inter-scale Resonance

Having established the scaling laws for size (Rₙ​) and speed (Cₙ​), we can now derive how frequency (νₙ​) must scale for the wave equation λₙ​νₙ​=Cₙ​ (where Rₙ​∝λₙ​) to hold at all levels.

From νₙ​∝Cₙ​/Rₙ​ and the established laws, we obtain:

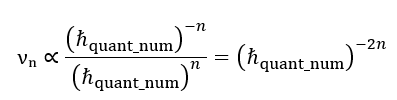
Thus, we arrive at the fundamental scaling law for frequency:

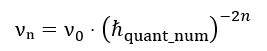
This means that frequency is not invariant but changes with the fractality level even more significantly than other parameters. For macro-levels (n=−1), the frequency decreases catastrophically. The principle of resonance, however, is not violated but refined. Resonance between fractal levels is possible not because their frequencies are identical, but because they are harmonically coherent (aligned) through powers of the same quantum, ℏ_quant​. This strict mathematical connection is the very mechanism that ensures self-similarity and interaction between the microcosm and the macrocosm.

7.8.6. Justification for the Scaling Exponents for Mass and Velocity

The choice of specific exponents (2n for mass, n for size, and −n for velocity) in the formulae for fractal transition is not arbitrary. It is a consequence of the need to simultaneously align several fundamental principles of this model:

1. Invariance of Energy: This scheme (Mₙ∝(ħ_quant)²ⁿ and Cₙ​∝( ħ_quant ​)⁻ⁿ) ensures the conservation of the total system energy, Eₙ​=Mₙ​Cₙ²​=mc².
2. Consistency with the Wave Equation: The chosen scaling laws for Rₙ​ and Cₙ​ uniquely determine the scaling law for frequency νₙ​, preserving the universality of the wave equation.
3. Consistency with Quantisation: The use of integer exponents n for all parameters ensures the ‘integral’ form of the quantum of action, ħ_quant ​, in energy relations at all levels, avoiding the appearance of fractional powers (roots), which corresponds to the fundamental principle of energy quantisation, E∝ℏν.

7.9 Frequency as the Fundamental Basis of Resonance, Perception, and the Multiplicity of ‘Worlds’

7.9.1. From Velocity to Frequency: Re-evaluating the Basis of Resonance

In developing this model, a key insight is the understanding of the role of frequency in physical processes. Whilst we initially proceeded from the constancy of the speed of light c as a fundamental factor, a deeper analysis shows that resonance – the universal mechanism of all interactions (Postulate 3.1) – is, in its essence, primarily related to frequency, not velocity. This is an elaboration of Postulate 3.3, which states: «The frequency of energy oscillations is a key parameter determining the possibility of resonant interaction…». It can be asserted that it is not speed that limits possible frequencies, but rather, a fundamental base frequency ν₀​ and the conditions for stable resonance to arise from it are what determine the entire hierarchy of characteristic speeds (Cₙ​), sizes (Rₙ​), and frequencies (νₙ​) at all fractal levels.

7.9.2. The Concept of ‘Worlds of Frequencies’

The analogy with waves in water illustrates how different, non-interacting wave systems can exist in the same medium. Developing this idea, one can hypothesise the existence of two types of a multiplicity of ‘worlds’:

1. Fractal Nesting within ‘Our World’: As shown in section 7.8, our observable world (characterised by a base speed c and a base frequency ν₀​) is itself fractal. It contains an infinite number of nested levels (n), each with its unique but harmonically related frequency νn​, which is determined by the scaling law νn​=ν₀​⋅(ℏ_quant​)⁻²ⁿ.
2. The Possibility of Other, Parallel ‘Worlds’: Who is to say that our base pair of constants (c and ν₀​) is the only one possible in the entire meta-Universe? If other fundamental interaction speeds existed, they would generate their own, completely independent fractal hierarchies, each with its own base frequency ν₀′​. Since their base frequencies would not be related to ours, these ‘worlds’ would not enter into resonance and would be unobservable to us.

7.9.3. Resonance as a Filter of Perception

This leads to a fundamental conclusion regarding the nature of our perception: We exist in our ‘world of frequencies’, which is defined by the base frequency ν0​ and its harmonics, set by the scaling law. Everything we observe and interact with is in resonance with us (as per Postulate 5.3). That which has a completely different base frequency simply does not exist for us; it passes through our world without leaving a trace. The consequences of this are that the world may be immeasurably more complex than we imagine, and the speed of light c is merely a characteristic of our ‘resonant layer’.

7.9.4. Horizons of Cognition

This theory, by proposing a mechanism for fractal transitions (e.g., state n=5 as an analogue of a black hole), allows one to ‘peer beyond the event horizon’ of our current level of perception, but only within our world of fractal levels, linked by a unified law of frequency scaling. What occurs in other, completely independent ‘worlds of frequencies’ remains beyond the scope of this model. However, the very supposition of their existence opens new horizons for the philosophical contemplation of reality and our place within it.

Conclusion

In this paper, an attempt was made to develop a unified conceptual and mathematical framework for describing physical reality — the «Theory of Wave Model of Matter and Fractal Structure of the Universe». Based on a small set of Postulates, centered on the notion of energy as a primary basis, Euclidean space as an active medium and resonance as a universal mechanism of interactions, a model was constructed that seeks to provide a physically explicit explanation of the fundamental properties of matter and laws of nature.

The key result of the work was the construction of the mathematical apparatus (Chapter 7), which made it possible to derive and calculate the basic parameters of the four stable elementary particles from first principles — standing wave geometry and the fundamental speed of light. Theoretical values for the basic masses (amplitudes M₀), characteristic wavelengths (λ₀) and diameters (d₀) for the neutrino, electron, neutron and proton, as well as for the elementary charge, were derived (Appendix 7).

During the analysis, it was found that the theoretical calculations for the «simple» wave structure of the electron show very good agreement with experiment. At the same time, for more «complex» nucleon structures (proton and neutron), small but systematic discrepancies were found. Further investigation of this phenomenon led to one of the central hypotheses of this paper, detailed in Appendix 7 (P7.5). It has been shown that this discrepancy may not be a flaw in the model, but a predictive consequence of the model. It is explained by the fact that our experimental standards (in particular, the atomic mass unit based on the carbon-12 ion) and, as a consequence, the measured fundamental constants (including Planck’s constant h_exp) are inherently calibrated to complex, coupled systems of nucleons rather than to «ideal» single particles. This «built-in» in the measurement system influence of structural features of complex particles explains the observed deviations.

The most significant confirmation of the validity of theoretical constructions was the result of fractal scaling described in Appendix 8. When the theoretical neutron wave size (≈1.6×10⁻¹³ m) derived in this model and the theoretical «scaling quantum» (ħ_quantum=1/| c⁴|ₙᵤₘ) were used to scale from micro- to macro-level (n=-1), the calculated size of the analog galaxy showed a strikingly good match with the observed size of the Milky Way. This not only eliminated a discrepancy of two orders of magnitude from the neutron size obtained in experiment, but also served as a strong argument in favor of the fact that the model correctly describes the «wave» rather than nuclear sizes of particles for the purposes of the fractal transition.

At the same time, the question of mass agreement during scaling remains open. Most likely, indirect mass determination introduces an error in the results obtained.

A discrepancy of one order of magnitude in the mass of the galaxy seems significant, but its interpretation requires caution, given the indirect nature of mass determination at all levels.

1. Indirect nature of the measurements: Just as the neutron mass is determined indirectly through nuclear reaction energies, the masses of galaxies are determined by dynamical effects (rotational velocities) rather than by direct «weighting». Both methods rely on existing models that may not account for all the structural and dynamical features predicted by this theory.
2. Evolution of experimental data: It is worth noting that experimental data on fundamental parameters can be significantly revised. For example, until recently (conventionally, until 2025), the size of the neutrino was estimated to be on the order of 10⁻¹⁹ m or less. However, recent studies of its «quantum extent» give a lower limit of 6.2×10⁻¹² m — an increase of seven orders of magnitude. This shows that our ideas about the parameters of the microcosm can change dramatically. It is possible that the current estimates of galaxy masses, especially their dark matter component, will be corrected in the future.
3. Complexity of the rotation structure: Current dark matter models that explain the rotation curves of galaxies often proceed from the simple assumption of a spherical halo. However, in this model, a spiral galaxy is analogous to a neutron, which has a complex internal rotation structure — «two vortices at the edges, swirled by one common vortex». Such complex dynamics (as opposed to a «single vortex» that could be analogous to a neutrino) can produce gravitational effects that are different from those of a simple spherical halo. It is possible that much less total mass is required to support such a complex rotational structure than current simplified models of dark matter predict.

It is also important to remember that when an object’s speed increases, its size decreases and its mass increases. This is something we can observe in practice.

Thus, the mass discrepancy may not indicate a flaw in the fractal principle, but rather that existing methods for estimating the mass of macroobjects do not fully account for the complex internal dynamics of wave structures predicted by this theory.

Thus, the proposed model is an internally consistent system that:

• Gives calculated values for the masses, sizes and charge of elementary particles from unified principles.
• Offers a physical explanation for discrepancies with experiment through structural features of measurement standards.
• Demonstrates predictive power through the example of fractal scaling.
• Provides a qualitative explanation for a wide range of phenomena, from the nature of fundamental forces to dark matter and quantum entanglement.

This work does not claim to be complete, but offers a new, intuitively clearer direction for thinking about the unity of physical laws, linking the microcosm and macrocosm through the universal principles of waves, resonance, and fractality.

The proposed model does not aim to disprove established physical theories, but offers a path to their integration and deeper physical understanding within a unified wave and fractal paradigm. It seeks to simplify the understanding of the world structure, offering an intuitively clearer picture where fundamental properties of matter and laws of nature are a consequence of universal energy dynamics.

Appendices

Appendix 1. Longitudinal waves of energy in the mechanism of electromagnetic wave propagation

Introduction

Usually electromagnetic waves are considered as transverse waves that do not require a medium for propagation. However, the very fact of their finite propagation speed makes us wonder: what happens to the energy in space during the wave’s motion? If energy cannot change instantaneously, it means that at some point in space there must be a gradient of its change. And if so, it is logical to assume that an electromagnetic wave generates not only transverse but also longitudinal fluctuations of energy.

In classical physics, the electromagnetic wave is described as strictly transverse. However, in the framework of the present model, which takes into account the finite propagation speed of interactions and the energy structure in space, it becomes necessary to introduce a longitudinal component associated with the energy density gradient. This does not cancel the classical picture, but extends it by describing additional subtle effects.

P1.1 Energy gradient and its implications

When an electromagnetic wave leaves the source, it changes the energy density in the surrounding space. As it propagates, the energy at the source point gradually returns to its original value, but at a distance R it remains changed. This means that there is an energy gradient between these points, which can propagate as a longitudinal wave. It is not considered in classical physics, but this does not mean that it is absent. Rather, its influence may be too subtle to be easily noticed.

We can put it another way: space, being energetically homogeneous at the beginning, becomes inhomogeneous after the wave passes through. And if the energy is redistributed, it means that there is a process that can be described as a longitudinal oscillation.

P1.2 Relationship to the de Broglie hypothesis

De Broglie introduced the idea that particles have wave properties, but did not give a specific mechanism of their formation. If a standing wave is indeed the basis of an elementary particle, then it is logical to ask: what exactly creates this wave? If an electromagnetic wave generates longitudinal energy fluctuations, then it is these that can stabilise the standing wave, making it a particle. Thus, a particle can be not just an abstract probability wave, but a real structure in space caused by wave processes.

P1.3 Conclusion

We are used to thinking that an electromagnetic wave is an exclusively transverse process. But if we consider it from the point of view of changes in energy density, it becomes obvious that transverse oscillations cannot exist in isolation. They inevitably cause longitudinal redistribution of energy, which opens new possibilities for understanding physical processes. Perhaps it is longitudinal waves of energy that will help explain not only the propagation of electromagnetic waves, but also the structure of particles and the nature of some unexplained phenomena. This does not require a revision of the whole physics, but gives an opportunity to look at the known processes from a different angle.

Appendix 2. Rethinking the Michelson-Morley Experience

One of the most famous experiments in the history of physics, the Michelson-Morley experiment, is traditionally interpreted as proof of the absence of the aether. However, what if this experiment does not reject the existence of the medium at all, but merely points to its unusual properties?

Albert Einstein created a very beautiful and coherent theory. It really describes everything very well. It is absolutely correct, so it cannot be refuted. It has only one drawback — it is difficult to understand and to describe. But it’s absolutely true. It also contains a postulate about the invariability of the speed of light, which is not explained in any way. And it uses the Lorentz transformation, which is also introduced as an axiom. These are flaws in the theory, which introduce a limitation on the understanding of the world.

The Michelson-Morley experiment (1887) was the decisive factor at that time. The wave nature of elementary particles had not yet been discovered at that time. At that time there was a wave theory of light, but the corpuscular-wave dualism had not yet been formulated. The very fact that light can behave as a particle began to be discussed later — at the beginning of the XX century.

Einstein, developing the special theory of relativity (1905), took as a basis the negative result of the Michelson-Morley experiment; his approach was to reject the ether concept rather than to consider the wave nature of matter. At that time it was accepted that light was an electromagnetic wave (according to Maxwell), but in a sense it was considered a separate nature from matter.

The reason why Einstein did not view everything as waves is that at that time there was neither experience nor mathematical apparatus to support this view. Corpuscular-wave dualism only began to take shape after 1924, when Louis de Broglie hypothesised the wave properties of matter. And quantum mechanics, which explained it, did not develop until the 1920s and 1930s.

Now, knowing the wave properties of matter, I propose to revisit the result of the Michelson-Morley experiment.

The Michelson-Morley experiment (1887) was conceived to discover the ether, a hypothetical medium in which light was then assumed to propagate, just as sound propagates in air.

Purpose of the experiment: To test whether there is a so-called «ether wind» — the movement of the ether relative to the Earth, which should affect the speed of light in different directions.

Basic idea: If the Earth moves through the ether:

• Light travelling along the Earth’s motion must travel the path in one time.
• Light travelling across has to travel the path in a different time.
• This should cause interference when comparing the two beams.

Michelson and Morley built an interferometer to compare the two beams.

The Michelson-Morley experiments did show small deviations, but:

• Small shifts of the interference pattern were recorded, about 10 times smaller than expected in the presence of an ether wind with the Earth’s velocity (about 30 km/s).
• These deviations were not of a magnitude or direction that could be explained by the motion of the Earth through the ether.

How the result was interpreted:

• Michelson and Morley considered these small deviations to be within the errors of measurement, and not evidence of an ether wind.
• The work was later repeated with increased precision (including by Michelson in the 1920s, as well as by Miller), and although Miller claimed to have found the effect, his results were not confirmed in other experiments.

I.e. experience has disproved the existence of ether. In the light of what we know from physics, we speak about particles as some point that behaves in space, obeying wave functions. But what if we extend the concept of a particle? Let’s give the particle a certain size in which the standing wave will be located. The size is fine, it does not contradict the known data in physics, but with the understanding of the standing wave there are uncertainties associated with the absence of a medium. In the previous chapter it was shown that the electromagnetic wave, due to the limitation of its propagation speed, must create a longitudinal wave, otherwise the limit of the propagation speed of electromagnetic interactions is violated. In this connection particles can be represented as longitudinal standing waves of energy in space.

If particles are waves of energy, then all matter is nothing but waves of energy in space. As we know, waves do not transport matter, but only energy. In this case, the Michelson-Morley experiment is not capable of creating and registering an «ether wind», since all we know is that it is waves of energy, in which case we can only study the energy itself. Of course, the presence of waves implies the presence of the medium, but since all we know is waves, we cannot influence the medium itself.

If we accept that everything in the world, including matter, observer, devices and light are forms of wave processes of energy in the structure of space, then the very question about the movement of the medium loses its meaning. If the medium is everything, there is no external background against which its motion could be fixed.

Even if this structure «moves», we, being a part of it, cannot measure it — because our metre, our clock, and light itself obey the same internal laws. Everything «floats» together, and there is no relativity within this structure.

This means that the negative result of the Michelson-Morley experiment does not at all exclude the existence of a structure in which waves propagate — it only shows that we cannot observe the absolute motion of this structure if we ourselves are waves of energy.

Conclusion

The Michelson-Morley experiment does not prove the absence of medium, but only shows that the Earth is not capable of creating an etheric wind because it is itself composed of waves. If elementary particles are waves and matter is their aggregate, then all matter is a wave structure.

That means:

• The speed of light remains the same because the speed of wave propagation is independent of the source.
• For construction of mathematical apparatus in physics, the ether is not necessary, as physics at the present moment is able to study only energy and its change.
• The forces of nature are wave processes of energy change because they are directly related to matter, which is a wave structure of energy.

The Michelson-Morley experiment confirms the wave nature of all matter, in which light and elementary particles simply follow the laws of wave propagation. That also speaks about impossibility to fix the motion of the medium from inside, if the matter itself is a wave form in this medium.

Appendix 3. Standing waves of energy and structure of elementary particles

Introduction

Modern physics describes elementary particles as point objects or perturbations of quantum fields, but another interpretation is possible. This chapter considers the structure of elementary particles as a longitudinal standing wave of energy, and their properties can be explained through de Broglie waves.

We will also consider how particle birth can be explained within this model and why the law of conservation of energy leads to the symmetry of matter and antimatter.

P3.1 Standing waves of energy density and particles

To date, science does not describe the origin of electric charge. What is its nature? Why is its value constant for elementary particles? Charge does not change its sign or its value regardless of the environment. Why does a change in velocity change the mass of a body, but nothing happens to the charge? What can be the cause of charge?

It is known that:

1/c = αћ/e²

where

e is the charge of the electron,

ћ is the reduced Planck constant,

c is the speed of light.

One constant is expressed through another constant.

Can be reviewed at the link (http://nuclphys.sinp.msu.ru/misc/constants.htm).

The physical quantity that is the inverse of speed is called pace. The pace shows how long it takes you to cover the desired distance.

This parameter is clearly a characteristic of an elementary particle, not an interaction, but a characteristic of a particle. It is clearly related to the rate from the speed of light. Question — what and how is overcome in the particle? What can we talk about?

It is necessary to understand what and where it is moving and why the tempo can take values «+1», «-1» and 0 (I have divided the tempo byαћ/e², because it is all a constant, but I have kept the sign of the charge, it will be very useful for us), let it be only numbers that tell us only about the direction. I.e.: «+1» means something is travelling somewhere at the speed of light in one direction, «-1» is movement in the opposite direction, and «0» is as if there is no movement in either direction.

As was shown in Chapter 7.1, the electromagnetic wave, being a transverse wave, also generates longitudinal waves of energy during its propagation. These two waves are interconnected. One propagates in the dimension of space, the other in the sphere. Energy fluctuations will occur in independent coordinates. It can also be said that the planes in which these two waves oscillate are orthogonal to each other, which means that to describe the overall process, both of these processes must be taken into account. The two processes will be related, but will be described in their own coordinates.

Since the particle is isolated in the dimension of space, it is logical to assume that it is a standing wave in the dimension of space. The particle is a standing wave, longitudinal, born by the propagation of an electromagnetic wave.

Let’s consider a few possible cases. First option:

Fig. 1 The first elementary particle, the neutral, neutrino

The wave has one node. The wave has run once up, and once down. The result is zero. This is the first and neutral particle. Let’s assume it’s a neutrino. If there is a standing wave node at the centre of the circle, the particle will be neutral. With an odd number of nodes the particle will be neutral, with an even number of nodes the particle will be «charged».

Fig. 2 Electron and positron

I will assume that this pair of particles is an electron and a positron. For the electron, the wave has travelled down twice and up once. Two of the beams are negative and one is positive. If we add them up, we get the tempo.

I think this is what characterises the tempo in the case of elementary particles. For the electron, it’s -1. For the positron, it’s +1.

Thus, the charge is related to the standing wave’s tempo. For standing waves, the tempo will be a number integer from the array {-1, 0, 1}. That’s why it is a constant. This is only true for standing waves, which can exist indefinitely. The important thing to understand is that it is not the electromagnetic wave itself, but the energy distribution wave in the region of space that the electromagnetic wave created during its propagation. In the following chapters it will be explained that in conditions of resonance, each half-wave of elementary particles will be geometrically responsible for the same work on the part of space to maintain it, which just so can later explain the constancy of charge, as well as its properties.

Let us interpret electric charge as a quantity that characterises the direction and magnitude of the work done by space in forming a standing wave. Thus, the charge is an internal characteristic of the wave structure due to the ratio of longitudinal and transverse energy fluctuations.

The characteristics that will eventually change are the radius of the circumference of the particle, the number of nodes or bundles, and the amplitude of the wave.

Now I will not explain about the principle of comparing the number of nodes and the name of particles, in the sequel I think it will become clear.

It is worth paying attention to the fact that for matter, «charged» particles in the centre always have a positive value of change in energy density on the space side. The amplitude of energy on the side of space increases, relative to some initial level, we can say there is a process of «compression». For antimatter, it is always negative. The energy of electromagnetic wave is spent on decreasing the amplitude of energy on the side of space, there is a process of «stretching» of space. You can see the relationship between tempo and charge. I have omitted the figures. The main thing is to understand the physics of the process. The increase of energy amplitude can be considered as a process of increasing energy density on the side of space, and the process of decreasing amplitude can be considered as a process of decreasing energy density on the side of space. Further in the text it is the phrases increase of energy density and decrease of energy density that will be often used.

Consider the following possible particle. Suppose that it is a proton and an antiproton:

Fig. 3 Proton and antiproton

It is known that the proton consists of three quarks in the case of the simple model. But also in some experiments and theories the proton can be considered as a system of five quarks. The five-quark (5-quark) model is used for a more accurate description of the internal structure and properties of the proton, but does not cancel the 3-quark basis. This is clearly seen when considering the structure of the proton as a wave of changing energy density. Quarks in this case, are nothing but half-waves of curvature of space, half-waves of change of energy density in a region of space. Therefore quarks by themselves cannot exist, the meaning of a standing wave is lost. These half-waves are different, three of one sign and two of the other. In this case, it turns out that the proton is made up of five quarks. The concept of quark is very convenient for describing the interactions within the atom, will help to describe the sublevels for electrons, will describe the absorption and release of energy in the form of quanta, at the transition of electrons on sublevels, as well as allow you to accurately calculate and describe the processes of nuclear reactions.

For «charged» particles, some gradient of density change in the region of space is formed at their boundary. The energy density will either increase or decrease. Hence there is an effect of interaction of «charged» particles. Like-minded particles repel, like-minded particles attract. This can be explained by the fact that the total energy density of the surrounding WORLD will try to minimise the distortions created by the density of particles at their boundary.

One should not also forget what the «charged» particle carries in its centre. This is very important. The difference of behaviour of matter and antimatter depends on the last factor. For matter in the centre of the particle there will be an increased energy density in the space area compared to the surrounding WORLD, which will lead to the gravitational effect and macro-objects will be created. In the case of antimatter the process will go the opposite way, all particles will try to «move away» from each other as far as possible. But at the same time antimatter will try to group at some distance from the matter particles. This will happen along the sphere. Later it will be clear that antimatter will accumulate along the boundary of the event horizon of the black hole of a larger scale.

A fuller description of these processes, as well as the birth principles of existing interactions, can be found in the philosophical work https://dzen.ru/a/ZoINoVGeh12vIl-E or https://zenodo.org/records/15291541 .

P3.2 De Broglie waves as the basis of particle structure

In the framework of the hypothesis of standing waves of energy density particles can be considered as nodes of such waves. The de Broglie wave associated with a particle does not simply describe its motion, but is its structural element. The de Broglie wavelength is determined by the relation:

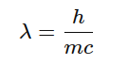
Where:

• h is Planck’s constant,
• m is the mass of the particle,
• c is the speed of light.

If a particle is a standing wave, its size must correspond to an integer number of half-waves, which explains energy quantisation.

There was an article written on this topic https://dzen.ru/a/Z7GBl8tL9DbB2x5L or https://zenodo.org/records/14883086 .

P 3.2.1 Results of calculations for the proton:

At the speed of light v=c the relativistic mass goes to infinity and the de Broglie wavelength tends to zero. However, if we consider a limiting approximation, for example, 0.9999999999999c, we can get a finite value. Let’s do the calculations.

Results for the proton at a velocity of 0.9999999999999c:

• De Broglie wavelength: 1.32×10⁻¹⁵ м
• Number of half-waves along the diameter (2r): 2.55

What’s interesting:

The number of half-waves remains finite. Moreover, in the variant proposed in the previous chapter, the proton is a standing wave with four nodes, which means that the number of half-waves should be equal to 2.5, which is very close to the calculated value.

So there’s a good chance that the de Broglie wave is nothing but a standing wave of energy in space.

If the de Broglie wavelength does describe the spatial structure of a standing wave, then:

The wavelength is not the electromagnetic wavelength, but the wave structure of space itself.

P3.3 Fractal structure of particles

If matter is viewed in terms of waves, we can assume the existence of similar structures, but with different scales. The phenomenon of resonance can do this. I.e. we can assume a fractal structure of the Universe. This means that at different levels of fractality particles can look the same. For example, if a neutron is a standing wave with three nodes, then a similar structure may appear on larger scales, such as the size of a galaxy. In the following, a formula will be presented that may be able to describe this process.

P3.4 Particle birth and the law of conservation of energy

P3.4.1 How particles are born

In the framework of the proposed model the birth of particles can be represented as a process of local redistribution of energy density. When in vacuum there arise fluctuations of energy density, they can lead to formation of stable standing waves, which are perceived as particles.

The birth of particles is accompanied by the formation of matter and antimatter particles. This follows from the law of conservation of energy: any local fluctuation must be compensated by an equal and opposite fluctuation.

P3.4.2 Why there is no symmetry breaking of matter and antimatter

It is usually considered that in the Universe there is an excess of matter over antimatter, but in the framework of this model symmetry breaking is not required. If a particle is a standing wave of energy density, its antipode may be a wave with opposite phase. The difference between matter and antimatter may lie in where the maxima and minima of energy density are located.

In a confined space, the redistribution of energy density will be due to the structure of the particles themselves:

• In the centre of matter particles (with an even number of nodes) there is a region with increased energy density, which leads to the effect of creating macro-objects and the emergence of gravity.
• In the centre of antimatter particles (with even number of nodes) there is a region with reduced energy density, which leads to their scattering from each other and formation of antigravity effect.
• Neutral particles are standing waves with an odd number of nodes. There is no density change at their centre, but they have the property of rotation. The antiparticle in this case differs only in the direction of rotation.

Antimatter is not capable of forming macroobjects because of the peculiarities of its structure. While matter particles tend to combine and can lead to the formation of black holes, antimatter is probably not capable of forming atoms more complex than antihydrogen. Instead, it would be distributed in a sphere around the forming black hole, contributing to the balance of energy in space.

Appendix 4: Lorentz transformation: classical derivation and wave interpretation

Introduction

Lorentz transformations play a key role in relativistic physics, describing how the spatial and temporal coordinates of objects change as they move. They were originally introduced as a mathematical tool to explain the invariance of the speed of light, but later became the basis of the special theory of relativity. However, if we consider particles as wave structures, we can arrive at the same transformations through a simple geometrical interpretation.

P4.1 How did Lorentz get his transformation?

The problem Lorenz was solving

Until the end of the 19th century, it was assumed that light propagates in the ether, a hypothetical medium that fills all space.

But the Michelson-Morley experiment (1887) showed that the speed of light does not depend on the motion of the Earth. This was strange: if the Earth moves through the ether, why does not the speed of light change?

Lorentz proposed that objects moving through the ether contract in the direction of motion.

P4.2 Length of the rod in a moving system

Lorentz imagined a rod of length L at rest.

• When it is stationary, its length is simply L.
• When it is travelling at velocity υ, the time at different points on the rod will not be the same due to relativistic time.

To find the new length L′, he used Lorentz transformations (named later in his honour).

P4.3 Output of length reduction

Consider two observers:

• One in a resting system (where the length of the rod is L).
• The second in a moving system (the observing rod moving with velocity υ).

Step 1: Write down the coordinates of the rod ends

• In the rest frame, the ends of the rod are at x₁ and x₂. Then its length is:

L=x₂-x₁

• In a moving system (a frame of reference moving with velocity υ) the coordinates are transformed by Lorentz formulas: x′=γ(x-υt)

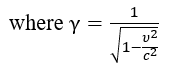
Step 2: Calculate the length of the rod in a moving system

Let us write down the new coordinates of the rod ends:

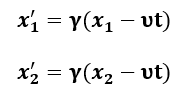
Subtract:

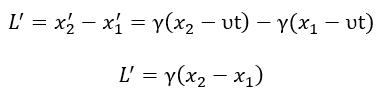
since x₂− x₁=L, we obtain:

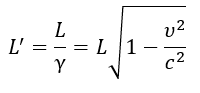
Where:

• L is the length of the object in the resting system,
• L’ is the length in the moving system,
• υ is the speed of motion,
• c is the speed of light.

P4.4 Formal mathematical reasoning

Using his coordinate transformations, Lorentz considered two observers:

• One is in a resting system where the rod has length L.
• The second moves with the rod and measures its length as L’.

He derived the length conversion based on the assumption that the speed of light is constant in any frame of reference and more time is required for a signal travelling in a moving system.

P4.5 Wave interpretation of length contraction

P4.5.1 Particle as wave

Instead of considering the particle as a point object, suppose it is a wave structure whose propagation in its own frame of reference is spherical at the speed of light c.

In this case, the particle has two velocities:

• The speed of wave propagation inside the particle (radial), which is c at rest.
• The velocity of the particle itself in space υ.

P4.5.2 Geometric relationship of velocities

If a particle moves, its internal wave structure changes. Since the total velocity cannot exceed c, the radial component of the velocity υ_sub decreases:

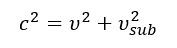
Hence:

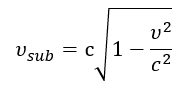
Since the size of a particle is determined by its internal wave, a reduction in this velocity means a reduction in the effective radius of the particle:

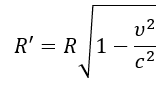
Since the length of an object is proportional to its radius, we get:

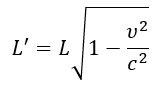
which corresponds exactly to the Lorentz formula!

P4.5.3 Conclusions

• Lorentz transformations can be obtained not only through mathematical postulates, but also through the wave nature of particles.
• Length contraction is a natural consequence of limiting the speed of light to internal motion in a particle.
• The wave interpretation makes relativistic effects understandable in terms of the physical structure of particles, not just axioms.

Appendix 5: Energy of a particle as a closed wave structure and the law of conservation of energy

Introduction

Modern physics considers elementary particles as objects possessing both corpuscular and wave properties. In relativistic mechanics the energy of a particle is defined by the expression:

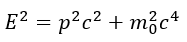
This formula shows that the energy of the particle grows with increasing momentum. However, if the particle is a closed wave structure of an electromagnetic wave and a standing wave in space created by the propagation of the electromagnetic wave, then its energy must be conserved within the system. This leads to an important question: how does a change in velocity affect the internal structure of the wave?

P5.1 De Broglie wavelength and energy redistribution

According to de Broglie’s hypothesis, a moving particle possesses an associated wave with length:

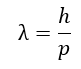
where h is Planck’s constant and p is momentum. An increase in velocity leads to an increase in momentum, and hence to a reduction in wavelength. This means that when a particle accelerates, its wave structure shrinks, changing the energy distribution within the system itself.

P5.2 Particle as a closed object

If a particle is a wave structure localised in space, its energy should not change, but only redistribute. Then:

• For an external observer, the energy of the particle grows due to the growth of momentum.
• Inside the particle system, the energy remains unchanged, changing only its configuration.

If the momentum increases with increasing velocity, the second term must decrease so that the total energy balance remains unchanged. This means that the de Broglie wavelength contraction is not just a consequence of motion, but a mechanism of energy redistribution inside the particle.

P5.3 Derivation of the energy equation

If we assume that the energy of a particle at change of its speed of motion is conserved, then in this case there should be its redistribution between wave components in space and along the sphere. We again obtain the equation of the circle, similar to the equation in the derivation of the Lorentz transformation:

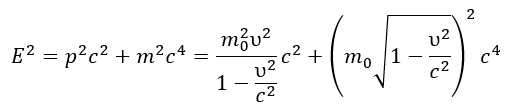
Let’s rewrite the second summand:

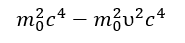
Then:

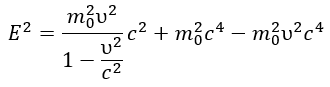
Let’s take out m₀²υ²c² in the first summand:

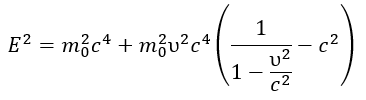
Now let’s solve the fraction:

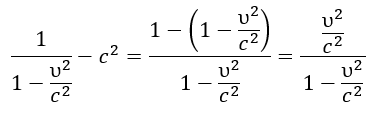
Then:

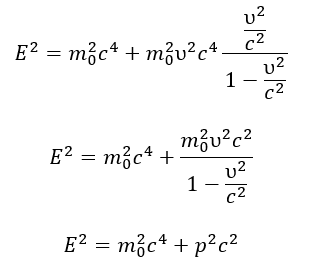
Thus, we end up with the same result as the standard relativistic expression, but we emphasise the splitting of the energy into two contributions:

• One depends on speed and resembles kinetic energy,
• The second reduces the internal energy of the particle as it accelerates.

If we consider the equation for energy in the form:

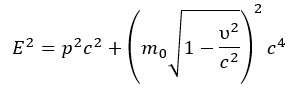
Then it becomes clear why the photon formally has no rest mass. It would be more correct to say that the summand responsible for the effective mass:

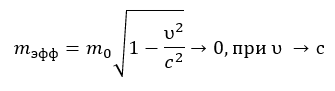
will tend to zero.

P5.4 Consequences

This conclusion confirms that the energy of the particle does not change at acceleration, but only redistributes:

• The first term expresses the momentum-dependent kinetic energy.
• The second term decreases the internal energy of the particle as the velocity increases.

Thus, the motion of a particle can be considered as a process of deformation of its wave structure, which naturally leads to relativistic effects without changing the total energy of the system.

Appendix 6. Wave resonance and scaling. The speed of light as a boundary of physical interactions.

Introduction

Modern physics operates with a number of fundamental constants, among which Planck’s constant h occupies a special place. However, if we consider the process of scaling physical quantities through resonant waves, we can assume that Planck’s constant is not an independent quantity, but is derived from the speed of light and geometrical characteristics of wave processes.

P6.1 Relation of wave processes and scaling

Many physical phenomena are based on resonance. If we consider standing waves at different scales, we can identify their common patterns. One of the key factors is that when scaling the wavelength, the number of nodes is preserved, while the frequency changes inversely proportional to the scale.

The speed of light plays here the role of a fundamental parameter determining the interaction of waves. It is important to note that the interaction velocity remains constant, but it can be decomposed into two components:

• along the x-axis (spatial scale that defines the size);
• along the y-axis (energy-related oscillation frequency).

This leads to a fundamental relationship between the size of the system and its frequency response.

P6.2 Wave resonance and scaling

Resonance occurs when wavelengths or multiples of wavelengths coincide, forming standing waves. In the fractal structure of nature this means that:

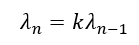
where k is the scaling factor between levels.

But an important point: mass and frequency are related, and we know that mass is expressed through the curvature of the wave.

We know that the energy of a single quantum is expressed through the wavelength:

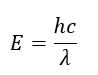
Now let’s find the energy density.

If the energy is distributed over a spherical volume, then:

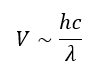
(Since for a spherical wave, the characteristic scale is the cube of the wavelength).

Then the energy density:

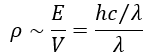
Now let’s look at the density:

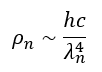
If resonance occurs between two levels n and n-1, their energy densities must be matched:

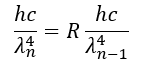
Where R is the transition coefficient between levels. From the resonance condition:

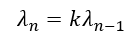
Then:

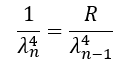
We substitute λₙ=kλₙ₋₁:

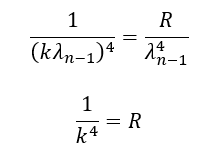
That is, the transition coefficient is related to scaling as:

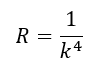
Since k is related to wavelength, and wavelength depends entirely on the speed of light, it is logical to assume that k is also related to the speed of light.

P6.3 Calculating Planck’s constant from the speed of light

Let R be the characteristic scale of the system associated with wave processes and k be the coefficient associated with the scaling frequency. Then we can write:

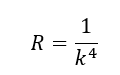
Taking k=|c|ₙᵤₘ, we obtain:

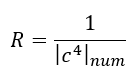
Substituting the exact value of the speed of light:

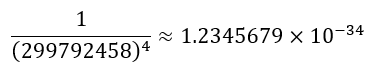
This value is extremely close to Planck’s reduced constant ℏ=h/2π, suggesting that it is not an independent fundamental constant but is determined through the speed of light and the geometry of wave processes.

Если:

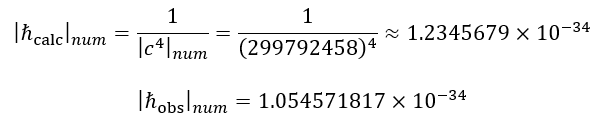
Then:

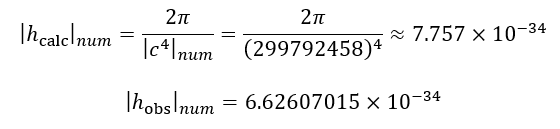
Of course, at the moment this is just an intuitive understanding of where Planck’s constant comes from. So far it’s just numbers, no dimensionality has been taken into account, but here we were deriving a general coefficient, which should be dimensionless by definition. But I think eventually all the constants can be expressed through the speed of light and geometry — in this case the connection comes from the geometry of the circle, the sphere. Since everything around is a wave process, only the speed of light and the π number are likely to be constants. All other constants are likely to be their derivatives.

Since the value of Planck’s constant was measured experimentally, it may contain some error. Taking this into account, we propose to consider the numerical value 1/|c|⁴ as a more accurate basic coefficient from which ℏ can be derived.

Conclusion

Thus, Planck’s constant can be related to wave resonance and scaling through the fundamental interaction speed — the speed of light. This gives a new understanding of quantum effects, connecting them with macroscopic regularities of wave systems. Further investigation of this hypothesis can shed light on the nature of quantum phenomena and the role of scaling in fundamental physics.

We can approach this question from a slightly different angle.

The space in which we live may have no limits, but there is a fundamental limit — the speed of light c. Even if space is infinite, the limiting speed of propagation of interactions imposes a natural limit on the processes occurring in it. This leads to the fact that physical systems cannot exist on arbitrary scales, but must obey certain resonance conditions.

P6.4 Four-dimensionality through a point

In all further calculations |ℏ|ₙᵤₘ means exclusively the numerical value of Planck’s constant abstracted from dimensionality. This allows one to establish possible geometrical relations between fundamental constants through the structure of space, without attempting an exact recalculation of physical units.

We usually say that the world is three-dimensional. However, there is another dimension, or another coordinate, which does not appear as a coordinate in the usual sense. This point is the centre of mass of the system. It plays a key role because:

• All matter interacts through centres of mass.
• Any system localises energy at a point, but the point itself has no size or space.
• Quantum mechanics confirms that energy collected at a single point is not bound to a particular scale of space.

Thus, we can speak about the fourth fundamental dimension, which determines not the coordinates, but the very principle of the organisation of matter.

P6.5 How do you describe a point as a scale centre?

In conventional physics, coordinates are given in 3D space (x,y,z), but if a point is not just a coordinate but a dynamic centre, then:

• The entire energy density must be expressed with respect to the distance to the centre r.
• The scaling of the energies must take into account not just the volume r³, but the interaction through the point itself.

Assumption: the energy around a point is distributed not just in three-dimensional space, but in such a way that an additional term appears in the scaling.

P6.6 Density of states around a point

Usually the density of states is expressed in terms of the volume of available phase space.

In 3D space:

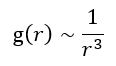
But if a point sets the centre of scaling, then we must consider that:

• The density of states «grows» towards the centre, but cannot become infinite.
• This means that an additional degree of scaling is added due to the interaction through the centre of mass.

Conclusion: if a point plays the role of a fundamental centre, then the possible states scale as:

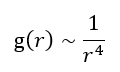
P6.6 How does this relate to the speed of light?

We know that r is related to c in the fundamental equations because distances are given through the rate of interactions.

If:

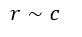
then we substitute that into the density of states:

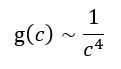
The density of states in the space with a centre point scales as 1/c⁴, which coincides perfectly with what we derived for ℏ! Here again we should note that the dimensionality is not taken into account here, but the proportionality factor is found. That is, we are only talking about the numerical value itself.

Combining the results of these two approaches, we obtain that the scaling factor is proportional to 1/c⁴. Since the constant bar is obtained experimentally, there are reasons to believe that some error may have been made in obtaining it. The value of the speed of light in this sense will be more correctly trusted.

P6.7 Restriction through the speed of light

Since space does not impose rigid boundaries, the only thing that limits physical processes is the limiting speed of interactions.

Wave processes in nature are always subject to the constraints of the medium. For example, sound in a pipe can only exist at certain wavelengths, and electromagnetic waves in a waveguide are also limited by geometry. But if our only limitation is the speed of light, then:

• It sets the natural scale of interactions.
• Any wave system must scale so that the limiting constraint is preserved.

In such a case the density of states of the wave process should depend not on the volume of space, but on the limiting velocity c.

Conclusion

• Space may be infinite, but the limitation of the speed of light creates natural limits to possible interactions.
• A point (centre of mass) is a fundamental dimension that determines the scaling of physical processes.
• The density of wave states in a system bounded by the speed of light leads to a law that is directly related to the speed of light as the fundamental limit of interactions.

Thus, quantum and gravitational effects may simply be a manifestation of a fundamental speed limit on interactions

Appendix 7: Calculation of particle parameters and experimental data.

We perform the calculation for all possible standing wave nodes and compare with the experimental data.

We use formulas from the chapter «7.1.3 Quantisation of knots and bounds of existence of particles»:

P7.1 n=1 (neutrinos):

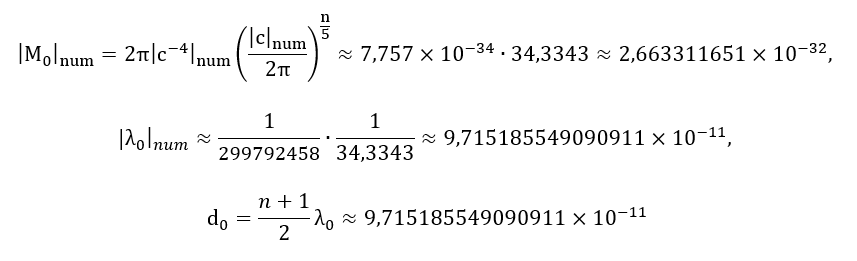
Taking into account chapter «7.7.6 Particularities of the neutrino mass», a correction for the measured mass in the experiment has to be introduced.

m₀≈6,581×10⁻³⁷

P7.2 n=2 (electron):

For the electron, the total mass is formed by only one centre half-wave, so nothing needs to be corrected.

m₀≈9,14429412189293×10⁻³¹

P7.3 n=3 (neutron):

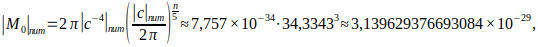
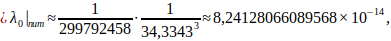
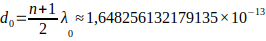
For neutrons, mass correction is not so obvious, so we will calculate it using the formula given in section 7.7.4, ‘Calculation of neutron mass (n=3) – taking into account internal rotation.’

We increase the amplitude by a factor of 3/2, then increase it by one quantum:

m₀≈3,139629376693084×10⁻²⁹×34,3343×1,5 ≈1,616954653622901×10⁻²⁷

P7.4 n=4 (proton):

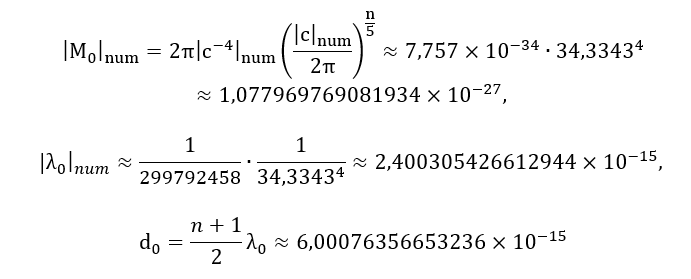
We have discussed the derivation of the proton mass in chapter «7.7.2 Transition to the mean distribution».

m₀≈1,077969769081934‬×10⁻²⁹×1,5 ≈1,616954653622901×10⁻²⁷

The experimental data was taken from the internet. Based on the data obtained, a table was drawn up:

n	name	λ₀ (m)	M₀ (кг)	m₀ (kg)	d₀ (m)	λ₀ exp (m)	m₀exp (kg)	d₀exp (m)
1	neutrino	9,715‬×10⁻¹¹	2,663×10⁻³²	6,581×10⁻³⁷	9,715‬×10⁻¹¹	10⁻⁶	<2.2×10⁻³⁷	10⁻¹⁰
2	electron	2,83×10⁻¹²	9,149×10⁻³¹	9,149×10⁻³¹	4,244×10⁻¹²	2.43×10⁻¹²	9.109×10⁻³¹	10⁻¹⁸
3	neutron	8,241×10⁻¹⁴	3,142×10⁻²⁹	1,617‬×10⁻²⁷	1,648‬×10⁻¹³	10⁻¹⁵	1.675×10⁻²⁷	10⁻¹⁵
4	proton	2,4×10⁻¹⁵	1,078‬×10⁻²⁷	1,617‬×10⁻²⁷	6,001‬×10⁻¹⁵	1.32×10⁻¹⁵	1.673×10⁻²⁷	10⁻¹⁵

P7.5 Assessment of possible distortion of fundamental constants due to integral effects

As has been shown in Table 4 and in the calculations of this appendix, the theoretical mass values derived from the wave model are close to the experimental ones but have small, systematic discrepancies. Specifically, the discrepancy for the electron is minimal (≈0.4%), whilst for nucleons it reaches 3-4%. Furthermore, the calculated mass of the neutron proves to be slightly greater than that of the proton, which corresponds with experimental findings, though the precise percentage ratio requires the introduction of correction factors. In this model, this discrepancy is not viewed as a flaw but as a consequence, indicating a difference between ‘ideal’ geometrical parameters and ‘effective’ quantities measured in experiments.

If we adopt the form of Planck’s constant proposed in this work as:

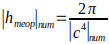
then, using the experimentally determined value of h, it can be seen that the corresponding value of the speed of light would have to be approximately 312,054,866 m/s, which is about 4% higher than the generally accepted value of 299,792,458 m/s. If this corrected speed of light is used in the quantisation coefficient, we obtain a mass value for the proton and neutron that is ideally suited to the experimentally determined mass of the neutron.

An interesting observation confirms this hypothesis. If we substitute the wave amplitudes M₀​ obtained in the model as mass into the classical de Broglie formula, the numerical values of the wavelengths prove to be identical to the theoretical λ₀​ only if we substitute into the de Broglie formula not the experimental Planck’s constant, h_exp​, but rather its theoretical expression from this model:

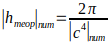
This may indicate that the experimentally obtained value h_exp​ represents an averaged or ‘effective’ quantity. The source of this effect may lie in the very definition of our mass standards.

The modern system of atomic masses and, consequently, the calibration of fundamental constants, rely on the carbon-12 ion, which by definition has a mass of exactly 12 atomic mass units. However, the carbon-12 nucleus is not an elementary particle, but a complex bound system of 6 protons and 6 neutrons. Its mass is determined not merely by the sum of the masses of its constituent nucleons, but also includes the immense contribution of the energy of their strong interaction (the so-called mass defect).

Thus, the standard for mass adopted is not a ‘pure’ elementary particle, but the result of their complex collective interaction. The complexity of this reference structure, the averaging of contributions from numerous protons and neutrons with their different (according to experiment) masses and binding energy, is inevitably ’embedded’ within the definition of the atomic mass unit.

Since all high-precision methods for measuring Planck’s constant (such as the Kibble balance) are ultimately calibrated against macroscopic masses composed of such complex nuclei, the measured value hexp​ is also an effective constant that reflects this structural complexity, rather than a ‘pure’ geometrical quantity like 2π/|c⁴|ₙᵤₘ​, which would correspond to an idealised, single wave structure.

This explains why the model presented here, proceeding from ‘ideal’ principles for single particles:

• Yields an almost perfect match for a ‘simple’ particle – the electron, whose contribution to the definition of the mass standard is minimal.
• Shows a small but systematic discrepancy for ‘complex’ particles – the nucleons, whose structural peculiarities and interactions form the very basis of the mass standard and, consequently, of h_exp​.
• Predicts that this discrepancy grows with the complexity of the particle (with increasing n), which is indeed observed when comparing the discrepancies for the proton and the neutron.

As a result, we are dealing with a closed system of physical measurements in which an ‘error’ or, more precisely, a ‘structural effect’ embedded in the definition of one of the fundamental quantities (mass via the carbon-12 ion) is translated to all other constants (including h_exp​) that are measured using it. This makes a consistent, yet potentially inexact (relative to ‘ideal’ geometrical principles), picture of physical parameters inevitable.

As for the wavelengths and sizes of elementary particles, there are still many uncertainties. Until recently, the size of the neutrino was considered to be smaller than 10⁻²² m, and only recently has its quantum extent been obtained: ≥ 6.2 picometres (6.2 × 10⁻¹² m), which is already comparable to the calculated size of 9.715 × 10⁻¹¹. To compare the values calculated here, it is the size of the quantum extension that will be best suited. Exactly it defines the wave structure of the particle, its size.

Here are links to recent studies that discuss the quantum extent of neutrinos:

1. Nature (2025): A lower limit on the spatial extent of the neutrino wave packet, 6.2 picometers, has been established for the first time. This value is much larger than the size of an atomic nucleus and reflects the quantum mechanical nature of neutrinos, where «size» refers to the spatial uncertainty of their wave packet rather than a physical measurement. InFocus Mail+1IXBT+1
2. Phys.org: The study confirmed that the spatial width of the neutrino wave packet is at least 6.2 picometres, which is thousands of times the size of an atomic nucleus. This discovery has important implications for understanding the quantum properties of neutrinos and could influence the development of more efficient neutrino detectors. phys.
3. CERN Courier: The BeEST experiment using unstable beryllium-7 nuclei has set the limit on the spatial localisation of the neutrino wave packet at 6.2 picometres. This value is more than 1000 times the size of an atomic nucleus and provides new constraints on the quantum properties of neutrinos. cerncourier..

Appendix 8: Scaling between the neutron and the Milky Way.

Based on the equation given in chapter «7.8 Fractality of the Universe structure.», the parameters of the neutron analogue will be calculated on a larger scale. The obtained values will be compared with the known parameters of the Milky Way galaxy. As Planck’s constant and neutron parameters the values obtained on experience are taken so that they better agree with the data obtained on experience for galaxies.

The size of the Milky Way:

• Diameter: estimates range from 100,000 to 120,000 light-years (about 30-37 kiloparsecs). znanierussia.ru
• Thickness: about 1,000 light years. techinsider.ru

The mass of the Milky Way:

• Total mass: estimates range from 1 to 2 trillion (10¹²) solar masses, including dark matter. ru.wikipedia.org
• Mass of the stellar component: about 50-60 billion (5-6 × 10¹⁰) solar masses.

P8.1 Size scaling

The diameter of the Milky Way in metres:

• Minimum estimate: ≈ 9.46×10²⁰ m
• Maximum score: ≈ 1.14×10²¹ m

The calculated radius of the Milky Way within this model differs slightly from the values accepted in astrophysics (~ 1×10²¹ m). This may be a consequence of several factors:

1. Experimental error in determining the size of both neutron and galaxy.
2. The effect of speed of movement on the size of objects, which is important to consider when comparing scales.
3. The calculation methods in astrophysics are based on models of the expansion of the Universe, which may introduce additional deviations. In the future we will consider the question of how correct it is to take into account the expansion when determining the sizes of objects.

It is also worth noting that the calculated theoretical size turned out to be slightly larger than that known from astrophysics, which is exactly how it should be. Baryonic matter is a consequence of changes in the internal redistribution of energy in standing waves on a galactic scale and will eventually gravitate towards the centre of the black hole, which will reduce its visible/occupied size. Which is, in fact, what is observed.

P8.2 Mass scaling

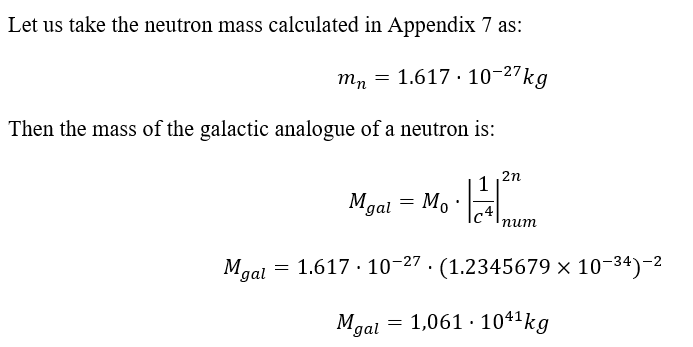
Milky Way mass derived from observations:

• Lower estimate: 1.99×10⁴² kg
• Upper estimate: 3.98×10⁴² kg

The mass was slightly less than expected (~ 3×10⁴² kg). This may be due to several factors:

1. Measurement errors arising in the determination of both neutron and galaxy masses.
2. Dependence of mass on speed of motion, which can play an important role when comparing objects at different scales.

It is also important to remember that when an object’s speed increases, its size decreases and its mass increases. This is something we can observe in practice.

P8.3 Analysing the results obtained

The calculated values of the radius and mass of the Milky Way galaxy, obtained on the basis of the fractal coefficient, showed a difference, but still an interesting approximation to the data of modern astrophysics. The radius calculated using the formula is R=1.335×10²¹ m, which is comparable to the observed value of about 1×10²¹ m. The mass obtained taking into account the fractal coefficient is M=1.061×10⁴¹ kg, while astrophysical estimates give a range of (1.99−3.98)×10⁴² kg. Although these results differ, they are still quite close to those obtained experimentally. However, it should be noted that the results obtained experimentally are indirect, which does not exclude errors in approximate calculations.

The question of the accuracy of current measurement methods remains important. In quantum physics, the mass of particles is determined through interaction with fields and depends on the environment. If spatial structures have fractal properties, this can affect measurement results, introducing systematic errors.

The results obtained indicate that the current methods of mass and size estimation both at the microscale and at the level of galaxies may need to be revised taking into account the fractal structure of the Universe. This opens prospects for refining experimental data and for a deeper understanding of the fundamental processes that shape the world at all scales.

P8.4 Scaling the speed of light

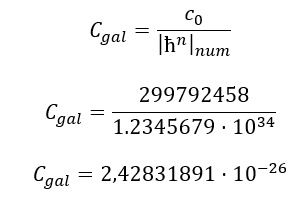
This shows that the speed of light — the limiting speed of electromagnetic interactions — is much smaller at the level of galaxies than at our scale, corresponding to a more rarefied state of energy.

P8.5 The Fractal Structure of the Universe: Galaxies as Elementary Particles

Obtained calculated data on the Milky Way using standard physical formulas with a slight modification and using again known in physics constant — Planck’s constant, can not be a simple coincidence. Of course, it would be possible to assume that it is just a coincidence, but if it was observed with only one parameter. But the fact that both parameters (mass and size) practically coincide already excludes the occurrence of coincidence. There is a strong possibility that the WORLD is fractal. The fact that for the Milky Way the fractalisation formula worked with astonishing accuracy suggests that the Milky Way is an analogue of the neutron. It’s a very good match. This can now be used to study and describe the space around us. The Milky Way galaxy can be taken as a reference.

It remains to be seen how to explain the large number of different kinds of galaxies. Find out whether they are all analogues of elementary particles, or whether some of them arise as a result of their joint interactions.

P8.6 Analogy between spiral galaxies and neutrons

The Milky Way and the Andromeda galaxy have similar masses but different sizes. This may be due to their speed: at lower speeds the galaxy becomes larger, and at higher speeds it becomes more compact. This difference explains the observed differences in size and mass. Moreover, the sizes of galaxies are determined by the visible matter, which will only be observed if the elementary particle is accelerated. If there is no acceleration, it will be difficult to track the size of the particle, as visible matter may not be present, or may not be present in sufficient quantity to determine the true size of the structure. Spiral galaxies are of particular interest because their structure and mass distribution obey certain regularities. When considering galaxies formed as standing waves with an even number of nodes (charged particles), it is difficult to determine the real size of the structure formed. It will consist of alternating regions with increased and decreased energy density. In the regions with increased energy density there may be matter. Interactions with such structures can lead to the formation of various types of galaxies, which are only indirect manifestations of the basic structures.

The cases of spiral galaxies with larger masses than the Milky Way are interesting. For example, ISOHDFS 27 is a spiral galaxy with a mass four times that of the Milky Way, but its size has increased only slightly. This behaviour may indicate that its mass increases by a multiple of the neutron (proton) mass, while its size changes only slightly. This is already reminiscent of nuclear interactions: ISOHDFS 27 is an object similar to a helium nucleus, where the energy density is higher and the mass increases by a multiple of the neutron mass.

P8.6.1 Compact dwarf galaxies and electrons

While spiral galaxies can be compared to neutrons or their interactions with protons, compact dwarf galaxies can be analogues of electrons. The electron can be thought of as a standing wave with a region of higher energy density at its centre. It is in this region that matter can form, which is what is perceived as compact dwarf galaxies. It is worth keeping in mind that the size of an electron refers to its effective size, as determined in scattering experiments. Interestingly, the difference between the size of the electron and neutron nucleus is three orders of magnitude. If the size of the Milky Way is estimated to be 10²⁰ — 10²¹ metres, the size of the electron’s analogue should be of the order of 10¹⁷ — 10¹⁸ metres, which corresponds to the size of compact dwarf galaxies.

P8.6.2 Formation of additional galaxies

There are many galaxies in the Universe, which may not be analogues of elementary particles, but may be the results of interactions between elementary particles of galaxy sizes. As a result of interactions can be formed zones with increased energy density, and given that it will also be accompanied by acceleration processes, it will lead to the emergence of matter in areas with increased energy density, which will give birth to galaxies. Such galaxies may seem to be independent objects, but probably they are just a consequence of redistribution of energy between more fundamental structures.

Thus, analyses of the sizes and masses of galaxies, as well as their interactions, can provide insight into the fundamental structure of the Universe and its analogy to the microcosm.

Appendix 9: Calculation of resonance frequencies of macroobjects within the wave geometric model of matter.

Introduction

In the theory of wave model of matter and fractal structure of the Universe, matter is considered as waves of energy. Everything is subject to resonant interaction. It is shown that there is a region of size 1/c² at the centre (considered as a dimensionless quantity), which can be seen as the centre of mass of a particle, and the adjacent region will have a wave energy distribution around it, which can be interpreted as a wave function. This helps to explain why the existing physics, quite accurately describes the processes taking place in the surroundings. This approach is very convenient for describing the world, although it has some limitations, for example, it does not allow to describe what is happening beyond the boundary of the event horizon. Also this approach can help to carry out calculations of resonance frequencies for macroobjects, using which it will be possible to obtain the necessary information, for example, frequencies accompanied or caused by seismic activity.

P9.1 Macro-object as a particle

Since the matter of which macroobjects are composed is the result of wave processes of energy, the macroobject can be replaced by a representation of a wave process. The macro-object itself will be an analogue of the region 1/c₁², where c₁ is the effective interaction velocity that would create an object with such dimensions.

In such a case, knowing the radius of the macroobject, one can find out the speed at which its analogue would be created as a whole wave. Knowing its effective interaction velocity, it is possible to calculate the charge of the object and the parameters of the particles that will be in resonance with it, which will allow, for example, to detect the effect of charge interaction or energy rotation and use it, for example, to repel from the macroobject.

If we have an object of radius R, we get a value for the interaction velocity:

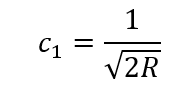
Knowing the effective rate of interaction, we obtain the expression from the formula for calculating the charge:

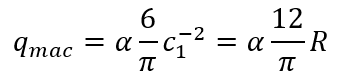
Using the formula for calculating the wavelength at a given interaction velocity, for a macroobject we can rewrite it in the form:

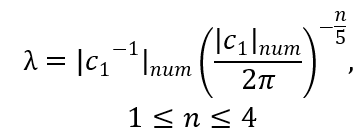
At n>4, energy transfer into gravitational waves will be observed, which will lead to seismic activity.

To calculate the frequency we use the standard formula:

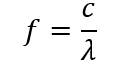
Here already the standard speed of light is used as c, because we have to get resonance with our interaction speed.

P9.2 Calculation for Earth

Using the formulas above, we calculate the parameters for the Earth.

Earth radius R 6371≈× 10³ m

According to current physical understanding, the Earth has a negative electric charge of approximately 600,000 coulombs (C). This charge is due to the existence of a global electric field between the Earth’s surface and the ionosphere, where the Earth is negatively charged and the ionosphere is positively charged. The average strength of this field near the Earth’s surface is about 130 V/m. ru.wikipedia.org ZFTSh, MIPT

It was this discrepancy between the values of the charge obtained by me and the one obtained in physics that made me think about the essence of the constant fine structure. This led to the formation of the chapter «On the nature of the constant fine structure», in which its essence is explained. For the Earth the influence of gravitation, caused by the same, in the manifestation of charge will be much less, so in this case there is a discrepancy. In the future I hope to find the calculated value of this coefficient depending on geometry.

Now let’s calculate wavelengths and frequencies for different numbers of nodes, which will create different variants of interactions at resonance with the Earth in this case.

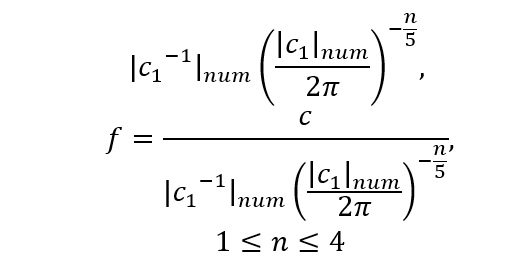
n=1

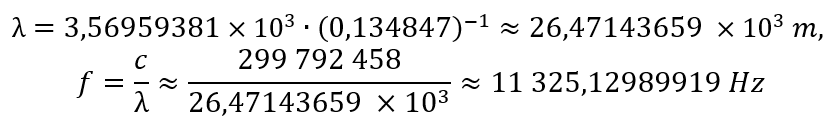
n=2

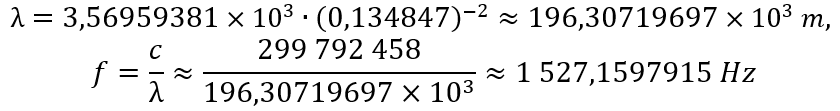
n=3

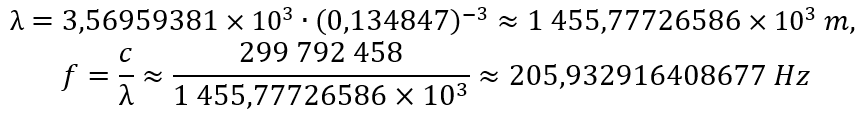
n=4

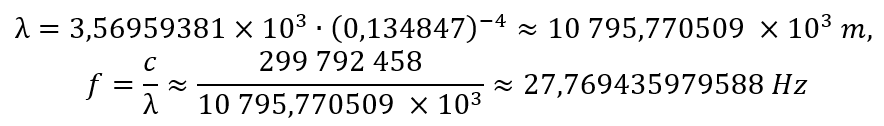
At frequencies lower than 27 Hz there will be energy transfer to the inner region of the macroobject, which can cause seismic activity. It can also be said that seismic activity will be accompanied by the emission of energy at frequencies of 27 Hz and below. This can be used as a signal of the beginning of seismic activity.

P9.3 Table of resonant wavelengths and frequencies for the Earth

P9.4 Conclusion

In this paper it is shown that using the geometrical approach of the wave model of matter, it is possible to calculate the resonance frequencies of macroobjects, including such as the Earth, without involving empirical data.

It has been shown that resonant frequencies corresponding to different numbers of nodes (n) can be used as indicators of different modes of interaction with a macroobject, from safe energy resonance to the transition to the region of gravitational disturbances and possible seismic activity.

These results confirm that the wave approach underlying the ‘Theory of wave model of matter and fractal structure of the Universe’ is applicable not only to the microcosm, but also to macroobjects, and can provide useful information about the structure and dynamics of interactions in nature.

The obtained dependences can be used both for further theoretical analyses and as a basis for the construction of practical devices interacting with mass at resonant frequencies.

The proposed calculations can be used as a basis for the development of technologies for controlling gravitational interaction and monitoring geophysical processes, as well as for the creation of means for wireless energy transfer at a distance with a high efficiency factor.

This approach offers a new perspective on the nature of mass and its relationship to electromagnetic processes. A more detailed discussion of this hypothesis and its philosophical implications can be found in the following works:

— (dzen.ru)

— (Zenodo)