1С-Рейтинг: Нефтебаза
Общая характеристика программы
Прикладное решение «1С-Рейтинг: Нефтебаза» предназначено для автоматизации деятельности предприятий, занимающихся оптовой и розничной торговлей нефтепродуктами.
Прикладное решение построено на основе типовой конфигурации «Бухгалтерия для Казахстана», что позволяет вести в одной информационной базе бухгалтерский, налоговый и оперативный учет финансово-хозяйственной деятельности предприятия.
В рамках данного материала рассматривается оперативный, бухгалтерский и налоговый учет нефтепродуктов. С возможностями типовой конфигурации «Бухгалтерия для Казахстана» можно ознакомиться в специальном разделе.
Программный продукт позволяет автоматизировать различные схемы оптово-розничной реализации нефтепродуктов, в том числе:
- реализация нефтепродуктов с нефтебаз;
- розничная реализация с автозаправочных станций;
- ответственное хранение;
- учет талонов и смарт-карт, отпуск по ним нефтепродуктов.
Основные возможности конфигурации:
- оперативный учет движения нефтепродуктов по местам хранения в разрезе Пин-кодов;
- ведение учета нефтепродуктов в мерах массы и объема, гибкая система пересчета по объемно-массовым показателям;
- набор документов, позволяющий отразить все необходимые операции по учету нефтепродуктов (покупка, учет доп. расходов, реализация, перемещение, списание, оприходование, возвраты, инвентаризация и т.д.);
- отражение в учете результатов розничной реализации нефтепродуктов через АЗС, пакетное формирование счетов-фактур по данным о розничной реализации;
- поштучный учет талонов на отпуск нефтепродуктов в разрезе серий, номеров, номиналов и сроков годности (реализация, возврат и погашение), автоматическое списание бланков при реализации талонов;
- учет выданных покупателям смарт-карт, поддержка денежных и литровых кошельков, отражение в учете и контроль движения нефтепродуктов по смарт-картам
- учет расчетов с бюджетом по акцизу в разрезе кодов бюджетной классификации, отражение исчисленного акциза по КБК в декларации по акцизу (форма 400.00);
- передача сырья в переработку и поступление нефтепродуктов из переработки;
- оформление сопроводительных накладных на нефтепродукты (СНН), экспорт СНН в файлы формата XML для последующего импорта в Web-приложение «Кабинет налогоплательщика», формирование реестров входящих и исходящих сопроводительных накладных;
- ответственное хранение нефтепродуктов (поступление на хранение и формирование актов приемки, переоформление между хранителями, отпуск и инвентаризация);
- формирование печатных форм первичных документов в мере массы и мере объема (в том числе счетов-фактур);
- набор настраиваемой пользователем специализированной отчетности, позволяющий всесторонне проанализировать результаты деятельности по обороту нефтепродуктов в различных разрезах;
- формирование деклараций по оптовой и розничной реализации нефтепродуктов, в том числе по структурным подразделениям и объектам налогообложения (в разные Налоговые комитеты);
- экспорт деклараций по оптовой и розничной реализации нефтепродуктов в файлы формата XML для последующего импорта в Приложение для Декларантов
Подсистема управления запасами нефтепродуктов позволяет автоматизировать учет движения стоимости горюче-смазочных материалов в разрезе Пин-кодов. Подсистема позволяет оформлять операции поступления (покупка, учет дополнительных расходов, импорт, возврат поставщику), реализации (счета на оплату, продажа оптом, оформление сопроводительных накладных, продажа через АЗС, возвраты от покупателей) и внутрискладского учета нефтепродуктов (перемещение, инвентаризация, оприходование и списание). Предусмотрена возможность ввода начальных остатков горюче-смазочных материалов, в том числе без отражения на счетах бухгалтерского учета.
Складской учет горюче-смазочных материалов, находящихся на ответственном хранении, ведется с использованием документов подсистемы «Ответственное хранение нефтепродуктов». При этом возможны следующие схемы ответственного хранения нефтепродуктов:
- горюче-смазочные материалы реализованы покупателю, но по каким-либо причинам, не могут быть сразу вывезены с нефтебазы;
- предприятие оказывает платные услуги ответственного хранения горюче-смазочных материалов в качестве дополнительного вида деятельности.
Подсистема учета талонов предоставляет возможность вести поштучный учет оборота талонов от момента реализации покупателю вплоть до погашения (отоваривания) или возврата, а также учитывать объем реализованных по талонам горюче-смазочных материалов в количественно-суммовом выражении.
По накопленным в конфигурации данным предусмотрено формирование специализированной отчетности, позволяющей всесторонне проанализировать результаты финансово-хозяйственной деятельности по обороту нефтепродуктов.
В составе конфигурации поставляется набор регламентированной отчетности, включающий декларации по оптовой и розничной реализации нефтепродуктов с возможностью выгрузки в формате XML в клиентское приложение для декларантов НК МФ РК.
При использовании конфигурации «1С-Рейтинг: Нефтебаза» совместно с конфигурацией «1С-Рейтинг: Налоговый мониторинг (МОП)», в состав конфигурации включается налоговая отчетность для предприятий, субъектов рынка нефтепродуктов, подлежащих электронному мониторингу с возможностью выгрузки в формате XML для приложения ИС МОП или СОНО.
Панель функций
«Панель функций» помогает начинающим пользователям быстрее осваивать программу, а опытным пользователям эффективнее выполнять ежедневные задачи. Разделы учета представлены на панели функций в виде схем работы, демонстрирующих типовую последовательность хозяйственных операций.
Общие принципы учета нефтепродуктов
Для оформления операций по движению товарно-материальных запасов, являющихся объектами учета нефтепродуктов, в конфигурации предусмотрен собственный набор документов, состав которого аналогичен документам типового решения «Бухгалтерия для Казахстана», но реализующий специфические требования к учету нефтепродуктов.
По сравнению с аналогичными документами типового решения, в табличные части документов подсистемы управления запасами нефтепродуктов добавлены специфичные реквизиты, позволяющие вести учет запасов нефтепродуктов в разрезе Пин-кодов, а также выполнять пересчет количества из меры массы (например, килограмм) в меру объема (например, литры), и наоборот.
Наиболее важной особенностью документов конфигурации является одновременное представление количества и цены для каждой номенклатурной позиции в двух единицах измерения: единице измерения массы и единицы измерения объема.
При объемно-массовых пересчетах используется показатель плотности нефтепродуктов, зависящий от температуры, при которой производятся замеры. Показатель плотности указывается в табличной части документов. По-умолчанию, значение реквизита принимается равным последнему значению плотности, установленному в каком-либо из документов (предшествующих данному) подсистемы управления запасами нефтепродуктов.
Помимо специфических реквизитов в табличной части, практически все документы подсистемы управления запасами нефтепродуктов содержат обязательный для заполнения реквизит шапки «Вид движения». Выбор вида движения в документе выполняется из справочника «Виды движения ГСМ», который используется для автоматического заполнения Деклараций по оптовой и розничной реализации нефтепродуктов.
Оптовая торговля нефтепродуктами
В «1С-Рейтинг: Нефтебаза» автоматизирован учет операций поступления и реализации нефтепродуктов, включая оптовую и розничную торговлю. Все операции по торговле нефтепродуктами учитываются в разрезе договоров с покупателями и поставщиками. При продаже нефтепродуктов выписываются счета на оплату, оформляются накладные и счета-фактуры. Автоматизировано отражение возвратов от покупателей и поставщиков. Обеспечивается автоматическое отражение торговых операций в бухгалтерском и налоговом учете.
Поступление нефтепродуктов
Поступление горюче-смазочных материалов по Пин-кодам поставщиков нефтепродуктов на склады (места хранения) предприятия, оформляется с помощью документа «ГСМ: Поступление».
Для оформления поступления горюче-смазочных материалов от поставщиков указывается вид операции «Покупка». При поступлении импортных горюче-смазочных материалов выбирается вид операции «Импорт». Поступление от структурных подразделений оформляется с видом операции «Поступление от структурного подразделения».
Для отражения в декларациях по оптовой и розничной реализации нефтепродуктов сведений о сопроводительных накладных, полученных от поставщиков нефтепродуктов, в документе предусмотрен набор реквизитов «Сопроводительная накладная».
Документ имеет две печатные формы, каждую из которых можно сформировать в мере массы или мере объема:
- З-3 (приходный ордер);
- Приходная накладная.
Для включения в стоимость поступивших горюче-смазочных материалов различного рода дополнительных расходов (например, услуг по доставке), связанных с их поступлением, используется документ «ГСМ: Поступление доп. расходов».
Для отражения информации о таможенных сборах и пошлинах, взимаемых при поступлении горюче-смазочных материалов по импорту на основании грузовой таможенной декларации, используется документ «ГСМ: ГТД по импорту».
Грузовая таможенная декларация может иметь несколько разделов, в которые группируются товары с одинаковым порядком расчета таможенных платежей. В табличной части раздела грузовой таможенной декларации, сведения о поступивших по импорту горюче-смазочных материалах вводятся раздельно по каждому Пин-коду. Взимаемые суммы таможенной пошлины, сбора, акциза и НДС распределяются пропорционально фактурной стоимости горюче-смазочных материалов.
Операции возврата горюче-смазочных материалов поставщикам оформляются с помощью документа «ГСМ: Возврат поставщику».
Документ имеет печатную форму «Возврат поставщику», которая может быть сформирована в мере массы или мере объема.
Реализация нефтепродуктов
Для оформления счета покупателю на предварительную оплату горюче-смазочных материалов или талонов для получения горюче-смазочных материалов на АЗС, используется документ «ГСМ: Счет на оплату покупателю».
Документ используется для получения печатных форм счета на оплату, регистрацию выставленных покупателям счетам, а также автоматического заполнения документов, вводимых на основании счета (реализация, платежное поручение входящее и т.д.).
Печатная форма «Счет на оплату» может быть сформирована в мере массы или мере объема.
Отгрузка структурным подразделениям и реализация покупателям горюче-смазочных материалов производится документом «ГСМ: Реализация».
В документе предусмотрен набор реквизитов «Реквизиты перевозчика», где можно указать сведения о водителе, транспортном средстве и прицепе, которые используются при формировании печатной формы и при заполнении сопроводительной накладной на основании документа реализации.
Если реализация введена на основании документов «ГСМ: Счет на оплату покупателю» или «ГСМ: Поступление», то табличная часть документа автоматически заполняется перечнем горюче-смазочных материалов из табличной части документов-оснований.
Документ имеет печатные формы «З-8 (накладная на отпуск запасов)» и «Расходная накладная», которые могут быть сформированы в мере массы или мере объема.
Сопроводительная накладная оформляется поставщиком в обязательном порядке при реализации и (или) отгрузке нефтепродуктов покупателям. Для оформления сопроводительных накладных в конфигурации предусмотрен документ ГСМ: Сопроводительная накладная.
Поскольку сопроводительные накладные являются бланками строгой отчетности и выдаются налоговыми комитетами, документ используется для печати на бланках данных сопроводительной накладной.
Указанный в документе номер бланка сопроводительной накладной (реквизит «Номер бланка») используется при формировании деклараций по оптовой и розничной реализации нефтепродуктов.
Для оформления операции возврата горюче-смазочных материалов от покупателей используется документ «ГСМ: Возврат от покупателя».
Если документ введен на основании документа «ГСМ: Реализация», то табличная часть документа автоматически заполняется перечнем реализованных горюче-смазочных материалов.
Документ имеет печатную форму «Возврат от покупателя», которая может быть сформирована в мере массы или мере объема.
Розничная торговля нефтепродуктами
Розничная реализация нефтепродуктов конечным потребителям осуществляется через автозаправочные станции. С определенной периодичностью, с автозаправочных станций в бухгалтерию, поступают отчеты за смену, содержащие объем реализованных в розницу горюче-смазочных материалов.
Для оформления операций розничной реализации нефтепродуктов через автозаправочные станции, предназначен документ «ГСМ: Реализация через АЗС».
Основным отличием документа реализации через АЗС от документа «ГСМ: Реализация» является наличие табличной части содержащей список покупателей, которым были реализованы нефтепродукты.
Реализация ГСМ через автозаправочные станции может производиться не только за наличный расчет, но и по талонам. Для отражения факта реализации ГСМ по талонам, в документе предусмотрен флаг «Реализация по талонам». Если данный флаг установлен, то при проведении документа, дополнительно формируются проводки по признанию доходом отчетного периода сумм, ранее отнесенных к доходам будущих периодов (при реализации талонов покупателю).
Документ «ГСМ: Реализация через АЗС» используется в подсистеме учета талонов и может вводиться на основании документа «ГСМ: Погашение талонов». Если реализация через АЗС введена на основании документа «ГСМ: Погашение талонов», то табличная часть документа автоматически заполняется перечнем горюче-смазочных материалов.
Документ имеет печатную форму «Расходная накладная», которая может быть сформирована в мере массы или мере объема.
Складские операции
Контроль за наличием и движением товарно-материальных ценностей предприятия — это одна из задач бухгалтерского учета, пересекающаяся с задачами складского учета. Эта задача решена в «1С-Рейтинг: нефтебаза». Реализован учет материалов, продукции и товаров на складах. Товарно-материальные ценности учитываются в разрезе позиций номенклатуры, партий и складов.
Важным отличием ведения складского партионного учета нефтепродуктов от бухгалтерского, является учет в разрезе Пин-кодов. Это отличие обусловлено тем, что нефтепродукты, поступившие от разных производителей, должны учитываться и отражаться в отчетности раздельно, по присвоенным Налоговым комитетом Пин-кодам.
Предусматривается проведение инвентаризаций товарно-материальных ценностей и автоматическая обработка их результатов. По результатам инвентаризации автоматически подсчитывается разница между учетным количеством (зарегистрированным в информационной базе при проведении документов поступления и отгрузки) и фактическим количеством ценностей, выявленным в результате инвентаризации. После чего оформляются документы списания (в случае недостачи) или оприходования (в случае выявления излишков).
Ввод начальных остатков
Если подсистема оптово-розничной реализации нефтепродуктов начинает использоваться на предприятии, имеющем остатки горюче-смазочных материалов, то необходимо ввести в учетные регистры сведения о начальных остатках с помощью документа «ГСМ: Ввод начальных остатков».
Перемещение между складами
Перемещение (передача) горюче-смазочных материалов между складами, например с нефтебазы на автозаправочные станции, оформляется с помощью документа «ГСМ: Перемещение».
В документе предусмотрен набор реквизитов «Транспортное средство», где можно указать сведения о водителе, транспортном средстве и прицепе, которые используются при формировании печатной формы и при заполнении сопроводительной накладной на основании документа перемещения.
Если документ введен на основании документа «ГСМ: Поступление», то табличная часть документа автоматически заполняется перечнем поступивших горюче-смазочных материалов.
Документ имеет печатную форму «Накладная на перемещение», которая может быть сформирована в мере массы или мере объема.
Инвентаризация нефтепродуктов
Целью проведения инвентаризации является проверка фактического наличия товарно-материальных запасов у материально-ответственных лиц и сверки полученных результатов с данными бухгалтерского учета. Для проведения инвентаризации горюче-смазочных материалов на складах (местах хранения) предприятия предназначен документ «ГСМ: Инвентаризация на складе».
Документ используется для печати инвентаризационной описи товарно-материальных запасов и сличительной ведомости результатов инвентаризации товарно-материальных запасов, а также оформления документов списания или оприходования горюче-смазочных материалов, соответственно, при выявлении недостач или излишков.
Оприходование нефтепродуктов
Оприходование горюче-смазочных материалов на склады предприятия, в том числе по результатам проведения инвентаризации, оформляется документом «ГСМ: Оприходование».
Документ может быть создан самостоятельно или введен на основании документа «ГСМ: Инвентаризация» на складе. В случае ввода документа на основании инвентаризации, табличная часть документа заполняется автоматически выявленными излишками горюче-смазочных материалов (при этом учитываются прочие документы оприходования, введенные на основании инвентаризации).
Документ имеет печатную форму «Накладная на оприходование товаров», которая может быть сформирована в мере массы или мере объема.
Списание нефтепродуктов
Для списания горюче-смазочных материалов со склада, в том числе по результатам проведения инвентаризации, предназначен документ «ГСМ: Списание».
Документ может быть создан самостоятельно или введен на основании документа «ГСМ: Инвентаризация на складе». В случае ввода документа на основании инвентаризации, табличная часть документа заполняется автоматически выявленной недостачей горюче-смазочных материалов (при этом учитываются прочие документы списания, введенные на основании инвентаризации).
Документ имеет три печатные формы, каждую из которых можно сформировать в мере массы или мере объема:
- Накладная на списание товаров.
- Акт списания.
- З-9 (Акт списания запасов).
Для отражения операций, связанных с исчислением акциза при списании товаров, используется документ «ГСМ: Регистрация прочих операций по подакцизным товарам».
Документ может быть введен как на основании документа на списание ГСМ («ГСМ: Списание»), в котором уже есть все основные данные о списанных товарах, так и путем ввода нового документа.
Специализированные отчеты по учету нефтепродуктов
Конфигурация «1С-Рейтинг: Нефтебаза» содержит набор специализированной отчетности, расширяющий возможности типового решения и предназначенный для анализа результатов деятельности предприятии по оптово-розничной реализации нефтепродуктов.
Отчет «Отчет по расчету акциза» позволяет получить развернутую информацию о начислении акциза по реализованным горюче-смазочным материалам.
В отчете выводятся сведения о количестве реализованных нефтепродуктов в мере массы и мере объема, суммах реализации и начисленного акциза.
Отчет «Отчет по движению подакцизных ГСМ» позволяет получить сведения о поступлении, реализации и возвратах горюче-смазочных материалов с детализацией по документам движения.
Отчет состоит из двух разделов: поступления и реализации горюче-смазочных материалов (с учетом возвратов).
В разделе поступления горюче-смазочных материалов выводятся сведения о поставщиках (наименование, РНН), номенклатурных позициях, приходной накладной, количестве и сумме.
Раздел реализации содержит сведения о покупателях (наименование, РНН), расходной накладной, номенклатурных позициях, количестве реализуемых нефтепродуктов с акцизом и без акциза, сумме реализации.
Отчет «Анализ движения ГСМ» разворачивает информацию по движению ГСМ в разрезе типов, видов движения, номенклатуры, ПИН-кодов. Количественные показатели движения ГСМ представлены в отчете как в мере массы, так и в мере объема.
Отчет «Отчет по реализации» позволяет получить детальные сведения о реализации горюче-смазочных материалов покупателям, оформленной документами «ГСМ: Реализация», «ГСМ: Реализация через АЗС» и «ГСМ: Возврат от покупателя».
В отчете выводятся сведения о реализованных и возвращенных номенклатурных позициях, оформленных счетах-фактурах и покупателях, ответхранении нефтепродуктов и т.д.
Отчет «Ведомость ГСМ по Пин-кодам» предназначен для анализа остатков и оборотов горюче-смазочных материалов по складам в разрезе Пин-кодов.
С помощью отчета можно получить информация по поступлению и отгрузке горюче-смазочных материалов со складов с любой периодичностью: день, неделя, месяц и т.д.
В отчет выводятся сведения о начальных и конечных остатках, поступление и списании в количественно-суммовом выражении.
Отчет «Реестр сопроводительных накладных» позволяет сформировать реестр сопроводительных накладных, оформляемых при реализации и (или) отгрузке нефтепродуктов.
В отчете выводятся сведения из документов «ГСМ: Сопроводительная накладная», сгруппированные по видам нефтепродуктов (бензин, дизельное топливо и т.д.).
В качестве полей отчета могут быть использованы дата, номер и номер бланка сопроводительной накладной, реквизиты покупателя, номенклатурные позиции и Пин-коды, плотность и вид нефтепродуктов.
Учет талонов
Среди предприятий, занимающихся розничной реализацией нефтепродуктов через сеть автозаправочных станций, распространена практика заключения договоров с покупателями на отпуск горюче-смазочных материалов по талонам.
Конфигурация предоставляет возможность вести поштучный учет оборота талонов от момента реализации покупателю вплоть до погашения (отоваривания) или возврата, а также учитывать объем реализованных по талонам горюче-смазочных материалов в количественно-суммовом выражении.
В общем случае талон содержит сведения о марке топлива, номинале (объем нефтепродуктов, подлежащих отпуску по данному талону), серию и номер, а также срок действия талона. Перечисленные реквизиты талона присутствуют в той или иной мере во всех документах подсистемы учета талонов.
Схема работы подсистемы учета талонов напоминает работу по предоплате. Приобретая определенное количество талонов, покупатель оплачивает необходимый объем нефтепродуктов, но фактической отгрузки и отражения в бухгалтерском учете при этом не происходит, то есть покупатель получает право на отгрузку горюче-смазочных материалов с автозаправочных станций. Далее, по мере фактической отгрузки горюче-смазочных материалов (например, заправки автотранспортных средств бензином), производится списание ГСМ со складов (АЗС) по бухгалтерскому учету и оформление отгрузочных документов (расходные накладные и счета-фактуры).
Выставление счетов на оплату
Для оформления счета покупателю на предварительную оплату талонов для получения горюче-смазочных материалов на АЗС, используется документ «ГСМ: Счет на оплату покупателю».
В документе вводятся сведения о заказанных покупателем талонах на горюче-смазочные материалы. Каждая строка табличной части представляет собой набор или пачку талонов, предназначенных для получения топлива одного вида (например, бензина), имеющих определенный номинал (например, 10 литров), серию и интервал номеров.
Реализация талонов
Реализация талонов покупателям для получения горюче-смазочных материалов на автозаправочных станциях предприятия отражается с помощью документа «ГСМ: Реализация талонов».
В документе вводятся сведения о реализуемых покупателю талонах. Каждая строка табличной части представляет собой набор или пачку талонов, предназначенных для получения топлива одного вида (например, бензина), имеющих определенный номинал (например, 10 литров), серию и интервал номеров.
В документе предусмотрена возможность автоматически списывать со склада (места хранения) бланки при реализации талонов покупателям.
Если реализация талонов введена на основании документа ГСМ: Счет на оплату покупателю, то табличная часть документа автоматически заполняется перечнем талонами из табличной части документа-основания.
В подсистеме учета талонов принята схема, по которой доход от реализации талонов признается в бухгалтерском учете в качестве доходов будущих периодов. Для отражения дохода от реализации талонов на счетах бухгалтерского учета, на закладке «Счет учета расчетов» помимо счета учета расчетов с контрагентом, указывается счет учета доходов будущих периодов. В дальнейшем, при оформлении операции реализации горюче-смазочных материалов с помощью документа «ГСМ: Реализация через АЗС», суммы, ранее отнесенные к доходам будущих периодов, признаются доходом отчетного периода (если в документе установлен флаг «Реализация по талонам»).
Возврат талонов
Если покупатель возвращает приобретенные ранее талоны, не отоваренные по каким-либо причинам (истек срок действия или покупатель решил использовать другую марку бензина), то для отражения операции возврата талонов в конфигурации предусмотрен документ «ГСМ: Возврат талонов».
В документе перечисляются талоны, по которым оформляется операция возврата от покупателя. В отличие от документа «ГСМ: Реализация талонов», одна строка табличной части соответствует одному талону.
Если документ ввести на основании документа «ГСМ: Реализация талонов», то табличная часть документа будет автоматически заполнена реализованными ранее талонами.
Отоваривание талонов покупателями
Для регистрации факта погашения поступивших в бухгалтерию с автозаправочных станций талонов, по которым была произведена отгрузка горюче-смазочных материалов покупателям, используется документ «ГСМ: Погашение талонов».
В документе перечисляются отоваренные талоны, по которым была произведена отгрузка горюче-смазочных материалов покупателям. В отличие от документа «ГСМ: Реализация талонов», одна строка табличной части соответствует одному талону.
Если документ ввести на основании документа «ГСМ: Реализация талонов», то табличная часть документа будет автоматически заполнена реализованными ранее талонами.
Документ не формирует движений по счетам бухгалтерского и налогового учета. Отгрузка горюче-смазочных материалов оформляется документом «ГСМ: Реализация через АЗС», который вводится на основании документа погашения талонов.
Отчетность по талонам
Отчет «Движения по талонам» позволяет проанализировать остатки и объем запланированной отгрузки горюче-смазочных материалов через автозаправочные станции по реализованным талонам, объем отгруженных горюче-смазочных материалов по погашенным талонам и объем не отгруженных горюче-смазочных материалов по возвращенным от покупателей талонам.
Отчет предназначен для анализа движения стоимости горюче-смазочных материалов и талонов в разрезе номиналов талонов (10 литров, 50 литров и т.д.).
Ответственное хранение нефтепродуктов
Предприятия, реализующие горюче-смазочные материалы с нефтебаз, могут предоставлять покупателям дополнительную услугу по ответственному хранению нефтепродуктов. При этом возможны следующие схемы ответственного хранения нефтепродуктов:
- горюче-смазочные материалы реализованы покупателю, но по каким-либо причинам, не могут быть сразу вывезены с нефтебазы. В этом случае документ, отражающий поступление на ответственное хранение, может быть введен на основании документа реализации. При этом табличная часть документа-поступления на хранение будет заполнена автоматически номенклатурными позициями, реализованными покупателю. Для случая возврата горюче-смазочных материалов от покупателя, предусмотрена возможность ввода на основании документа-возврата документа, отражающего отпуск с ответственного хранения. Табличная часть документа отпуска с хранения также будет заполнена автоматически возвращаемыми номенклатурными позициями;
- предприятие оказывает платные услуги ответственного хранения горюче-смазочных материалов в качестве дополнительного вида деятельности. В этом случае документ, отражающий поступление на ответственное хранение, вводится самостоятельно. При отпуске горюче-смазочных материалов с хранения, документ отпуска может быть введен и заполнен автоматически на основании документа-поступления на хранение.
Поступление нефтепродуктов на ответственное хранение
Поступление горюче-смазочных материалов на хранение по договорам ответственного хранения оформляется с помощью документа «ГСМ: Поступление на хранение».
В документе присутствуют реквизиты для регистрации данных акта слива по поступившим на хранение ГСМ: номер и тип цистерны, высота взлива, температура, данные накладной и т.д., а также возможно формирование печатной формы «Акт приемки нефтепродуктов». Предусмотрена возможность удерживать ГСМ за хранение, а также списывать естественную убыль ГСМ по хранению.
Переоформление нефтепродуктов на хранении
Для регистрации операций переоформления нефтепродуктов с одного хранителя на другого в прикладном решении используется документ «Переоформление ГСМ на хранении».
В документе указывается склад, на котором регистрируется переоформление, хранитель и договор хранения – отправитель, хранитель и договор хранения – получатель.
Документ может быть введен и автоматически заполнен на основании документа «Поступление ГСМ на хранение».
Отпуск нефтепродуктов с ответственного хранения
Для отражения операции отпуска горюче-смазочных материалов с ответственного хранения по окончанию срока хранения или при возврате от покупателя, используется документ «ГСМ: Расход с хранения».
При отгрузке горюче-смазочных материалов по окончанию срока хранения, документ может быть введен на основании «ГСМ: Поступление на хранение». В этом документ будет автоматически заполнен номенклатурными позициями, поступившими ранее на ответственное хранение.
В случае отпуска с ответственного хранения в результате возврата горюче-смазочных материалов покупателем, документ может быть введен на основании «ГСМ: Возврат от покупателя». В этом случае документ будет автоматически заполнен возвращенными покупателем номенклатурными позициями.
Инвентаризация нефтепродуктов на хранении
Для нефтепродуктов, находящихся на ответственном хранении, добавлена возможность регистрировать в информационной базе результаты проведения инвентаризации с помощью документа «ГСМ: Инвентаризация на складе».
Отчетность по нефтепродуктам на хранении
Отчет «Ведомость хранения ГСМ» предназначен для отражения остатков ГСМ на хранении с детализацией по складам, номенклатуре и хранителям на указанную дату.
Отчет «Отчет по поступлению на хранение», предназначен для детального анализа дополнительных сведений о поступивших на хранение ГСМ (номера цистерн, взлив, температура, плотность и т.д.). Показывает количество отгруженных ГСМ как в мере массы, так и в мере объема.
Отчет «Отчет по отгрузке с хранения» разворачивает информацию по отгрузке ГСМ с хранение в разрезе складов, номенклатуры, контрагентов, водителей и гос. номеров транспортных средств. Показывает количество отгруженных ГСМ как в мере массы, так и в мере объема.
Налоговая отчетность
В поставку конфигурации входит набор отчетности «Декларант», расширяющий состав регламентированных отчетов типового решения «Бухгалтерия для Казахстана». Набор отчетности конфигурации включает:
- Декларации по оптовой реализации нефтепродуктов:
- Форма 3.1 Баланс оборота нефтепродуктов оптовых поставщиков нефтепродуктов.
- Форма 3.2 Сведения о поставках нефтепродуктов оптовых поставщиков нефтепродуктов.
- Форма 3.3 Сведения о реализации и отгрузке нефтепродуктов оптовых поставщиков нефтепродуктов.
- Форма 3.4 Баланс оборота нефтепродуктов структурного подразделения оптового поставщика нефтепродуктов.
- Форма 3.5 Сведения о поставках нефтепродуктов структурного подразделения оптового поставщика нефтепродуктов.
- Форма 3.6 Сведения о реализации и отгрузке нефтепродуктов структурного подразделения оптового поставщика нефтепродуктов.
- Декларации по розничной реализации нефтепродуктов:
- Форма 4.1 Баланс оборота нефтепродуктов розничного реализатора нефтепродуктов.
- Форма 4.2 Сведения о поставках нефтепродуктов розничного реализатора нефтепродуктов.
Интеграция с «1С-Рейтинг: Налоговый мониторинг (МОП)»
Производители нефтепродуктов, поставщики нефти и лица, осуществляющие реализацию нефтепродуктов с баз, предоставляют в налоговые комитеты отчетность по основным финансово-экономическим показателям субъектов рынка нефтепродуктов, подлежащих электронному мониторингу. Для обеспечения возможности автоматического формирования отчетности субъектов рынка нефтепродуктов, в типовое решение может быть дополнительно встроена конфигурация «1С-Рейтинг: Налоговый мониторинг (МОП)».
Конфигурация «1С-Рейтинг: Налоговый мониторинг» позволяет автоматизировать процесс формирования отчетов по основным финансово-экономическим и налоговым показателям деятельности крупных предприятий, являющихся хозяйствующими субъектами или субъектами рынка нефтепродуктов и подлежащих электронному мониторингу. Прикладное решение обеспечивает возможность выгрузки отчетности в формате XML для программного обеспечения по системе Мониторинг крупных предприятий (ИС МОП или СОНО).
Интеграция с «1С-Рейтинг: Управление затратами на автотранспорт. Путевые листы»
В конфигурацию «1С-Рейтинг: Нефтебаза», в качестве подсистемы управления затратами на автотранспорт, интегрировано отраслевое решение «1С-Рейтинг: Управление затратами на автотранспорт. Путевые листы». Подробнее с возможностями отраслевого решения «1С-Рейтинг: Управление затратами на автотранспорт. Путевые листы» можно ознакомится в специальном разделе конфигурации.
Функциональные возможности подсистемы управления затратами на автотранспорт:
Учет ГСМ
Подсистема управления затратами на автотранспорт позволяет вести учет выдачи и слива ГСМ, выполнять расчет нормы расхода и списание ГСМ, вести учет остатков ГСМ в баках транспортных средств и выполнять их инвентаризацию.
Учет выданных ГСМ ведется по маркам ГСМ, транспортным средствам и способам выдачи. Сведения о количестве выданных ГСМ регистрируются в документе «Заправочная ведомость» или непосредственно в документе «Путевой лист». Выбор документа для оформления выдачи ГСМ обусловлен учетной политикой предприятия. Учет количества ГСМ в баках транспортных средств ведется в разрезе марок ГСМ, транспортных средств водителей и способов выдачи (например, выдача со склада, талонами, смарт — картами и т.д.).
Слив ГСМ оформляется документом «Слив ГСМ с транспортного средства».
На основании сведений об объеме выполненных работ (таких как пробег, отработанное время, количество технологических операций и т.д.), норм расхода и различных коэффициентов, учитывающих специфику эксплуатации транспортных средств, в документе «Путевой лист» выполняется расчет нормы расхода по произвольным формулам. Для расчета могут использоваться как предопределенные формулы расчета, так и формулы, добавленные пользователем.
На основании рассчитанной нормы расхода выполняется списание ГСМ документом «Списание ГСМ» или непосредственно в документе «Путевой лист». Выбор документа для оформления списания ГСМ обусловлен учетной политикой предприятия. Схема отражения затрат на ГСМ может быть при необходимости установлена в каждом путевом листе отдельно, что позволяет повысить точность расчета затрат при расчете себестоимости готовой продукции.
Для инвентаризации фактического наличия ГСМ в баках транспортных средств используется документ «Акт замера ГСМ в баках».
Специализированная отчетность позволяет проанализировать движение и остатки ГСМ в баках транспортных средств.
Сведения о выдаче, сливе и списании ГСМ отражаются в бухгалтерском, налоговом и управленческом учете.
Учет выработки транспортных средств и водителей
В подсистеме реализована возможность учета выработки транспортных средств и водителей. При оформлении в учетной системе документа «Путевой лист» может быть зарегистрирована информация о выработке транспортных средств и водителей. Список доступных параметров выработки задается пользователем. Для транспортных средств параметрами выработки могут быть пробег, отработанные моточасы и т.д. Для водителей параметрами выработки могут быть основное отработанное время, время в наряде, ночные часы и т.д.
Специализированная отчетность позволяет проанализировать зарегистрированную выработку по отдельным параметрам за период.
Расчет зарплаты водителей
Подсистема расширяет возможности расчета заработной платы типовой конфигурации, позволяя начислять зарплату водителям сдельно на основании выработки, зафиксированной в путевых листах. Расчет выполняется автоматически по произвольным формулам. Формулы расчета устанавливаются отдельно для каждого вида начислений.
Учет шин и аккумуляторов
Подсистема предоставляет средства учета шин и аккумуляторов, устанавливаемых на транспортные средства. Учет ведется по серийным номерам. Для отражения в учете операций монтажа/демонтажа комплектующих используется документ «Ремонтный лист транспортного средства», где можно указать сведения о месте установки комплектующего, выработке на момент монтажа/демонтажа и техническом состоянии. Для регистрации износа шин и аккумуляторов используется механизм регистрации выработки транспортных средств в документе «Путевой лист». Т.е. выработка транспортного средства автоматически может быть отнесена к комплектующим, установленным на данное транспортное средство.
Для получения сведений о наличии комплектующих, установленных на транспортные средства и степени их износа, предназначен отчет «Остатки комплектующих на транспортных средствах». Отчеты «Карточка учета автопокрышки» и «Карточка учета аккумулятора» используются для отражения истории эксплуатации комплектующего: когда и на какие транспортные средства устанавливалось комплектующее, выработка с начала эксплуатации и за период работы на транспортном средстве и т.д.
Внимание! Для работы с подсистемой управления затратами на автотранспорт в конфигурации «1С-Рейтинг: Нефтебаза» необходимо приобрести лицензию на прикладное решение «1C-Рейтинг: Управление затратами на автотранспорт. Путевые листы».
Преимущества «1С-Рейтинг: Нефтебаза» на платформе «1С: Предприятие 8»
По сравнению с предыдущей версией программа «1С-Рейтинг: Нефтебаза 8» обладает рядом существенных преимуществ, связанных как с использованием возможностей новой технологической платформы, так и с развитием функциональности и эргономики прикладного решения.
| 1С-Рейтинг: Нефтебаза |
1С-Рейтинг: Нефтепродукты |
| Товарно-материальные запасы |
| Общие положения |
| Параллельно бухгалтерскому учету ведется оперативный учет остатков и оборота нефтепродуктов. Оперативный учет предоставляет более широкие аналитические возможности по сравнению с бухгалтерским, за счет чего пользователь получает возможность более полно и глубоко анализировать сведения о движении нефтепродуктов.
Для пользователя наличие двух параллельных видов учета является абсолютно прозрачным за счет того, что документы по учету нефтепродуктов одновременно отражаются в бухгалтерском и оперативном видах учета. |
Предусмотрено ведение только бухгалтерского учета остатков и оборота нефтепродуктов.
Дополнительные аналитические разрезы, учитывающие специфику работы с нефтепродуктами, организованы с использованием забалансового учета. |
| Реализована возможность настройки порядка оценки запасов по Пин-кодам, являющихся нефтепродуктами, для целей ведения бухгалтерского учета. С помощью параметра «Вести оценку запасов нефтепродуктов в бухгалтерском учете по Пин-кодам» учетной политики по ГСМ, определяется будет ли при списании нефтепродуктов по бухгалтерскому учету рассчитываться себестоимость в разрезе Пин-кодов или в целом по номенклатуре.
По-умолчанию, в конфигурации принят порядок оценки запасов в бухгалтерском учете по Пин-кодам. При данном подходе стоимость запасов по оперативному и бухгалтерскому учету совпадает и определяется по данным оперативного учета.
В оперативном учете нефтепродуктов себестоимость списания всегда определяется в разрезе Пин-кодов. |
При использовании метода расчета себестоимости по партиям («FIFO» или «LIFO»), оценка запасов в бухгалтерском учета ведется в разрезе Пин-кодов нефтепродуктов, т.к. в этом случае для каждого Пин-кода создается отдельная партия, даже в пределах одного партияобразующего документа.
При использовании средневзвешенного метода расчета себестоимости («По среднему»), оценка запасов в бухгалтерском учете ведется в пределах номенклатурной единицы. |
| Работа с документами |
| Предусмотрена возможность для каждой единицы измерения настраивать порядок округления результата при выполнении объемно-массовых пересчетов в табличных частях документов по учету ГСМ. |
Для каждой организации можно указать значение «Количество знаков после запятой», определяющее разрядность реквизита «Количество» в табличных частях документов реализации ГСМ. |
| В формах всех документов по учету нефтепродуктов одновременно выводятся сведения о единице измерения, цене и количестве нефтепродуктов в мере массы и мере объема. |
В документах «Реализация ГСМ», «Реализация ГСМ через АЗС», «Сопроводительная накладная», «Счет на оплату» одновременно выводятся сведения о единице измерения, цене и количестве нефтепродуктов в мере массы и мере объема.
В остальных документах сведения выводятся только в одной мере, указанной в качестве меры расчета документа, либо в базовой единице измерения (указанной в карточке номенклатуры). |
| В формах всех документов по учету нефтепродуктов предусмотрен выбор меры ввода данных (масса или объем).
Выбранное значение оказывает влияние на объемно-массовые пересчеты, установку цен и порядок следования колонок табличной части документа.
При этом сохраняется возможность изменения сведений как в мере объема, так и в мере массы, независимо от выбранной меры ввода данных. |
В документах «Возврат от покупателя ГСМ», «Реализация ГСМ», «Реализация ГСМ через АЗС», «Сопроводительная накладная» и «Счет ГСМ» предусмотрен выбор меры расчета.
Выбранное значение влияет на доступность реквизитов меры массы или меры объема. Если указана мера массы, то сведения в мере объема определяется расчетным путем и наоборот. |
| Для отнесения на себестоимость расходов по перемещению материальных запасов (нефтепродуктов) между местами хранения реализован ввод и автоматическое заполнение документов «Поступление доп. расходов» на основании документов «Перемещение ГСМ». Например, можно относить на себестоимость перемещаемых нефтепродуктов услуги по транспортировке нефтепродуктов с нефтебазы на АЗС. |
Не предусмотрен |
| Для документов «Реализация ГСМ», «Перемещение ГСМ» и «Сопроводительная накладная» предусмотрена возможность формирования печатной формы товарно-транспортной накладной. |
Не предусмотрено |
| Счета-фактуры |
| Реализована возможность множественного ввода счетов-фактур выданных на основании документа «Реализация ГСМ через АЗС». Ввод счетов-фактур производится отдельно для каждого покупателя непосредственно из строки табличной части «Контрагенты» документа «Реализация ГСМ через АЗС» |
На основании документа «Реализация ГСМ через АЗС» может быть введен только один счет-фактура, независимо от количества покупателей, указанных в табличной части «Контрагенты» документа. |
| Реализован инструмент пакетного формирования счетов-фактур выданных на основании документов «Реализация ГСМ через АЗС». Инструмент позволяет пакетно создавать, печатать и проводить счета-фактуры по данным о розничной реализации ГСМ через АЗС. |
Не предусмотрено |
| Отчетность |
| Отчет «Анализ движения ГСМ» позволяет проанализировать в различных разрезах движение нефтепродуктов по складам одновременно в мере массы и мере объема по показателям плотности, указанным в документах движения.
Настраивается состав выводимых в отчет показателей и полей, оформление отчета, отбор, сортировка и группировка по произвольным полям. |
Движение ГСМ можно проанализировать с помощью стандартной бухгалтерской отчетности по счетам учета ТМЗ в разрезе доступных для счета субконто, либо по забалансовому счету «ДТ» в разрезе Пин-кодов и мест хранения нефтепродуктов. |
| Отчет «Ведомость ГСМ по Пин-кодам» предназначен для анализа остатков и оборотов нефтепродуктов одновременно в мере массы и мере объема по складам.
Настраивается состав выводимых в отчет показателей и полей, оформление отчета, отбор, сортировка и группировка по произвольным полям. |
Остатки и обороты ГСМ можно проанализировать с помощью стандартной бухгалтерской отчетности по счетам учета ТМЗ в разрезе доступных для счета субконто, либо по забалансовому счету «ДТ» в разрезе Пин-кодов и мест хранения нефтепродуктов. |
| Отчет «Отчет по движению подакцизных ТМЗ» позволяет получить сведения о поступлении, реализации и возвратах нефтепродуктов с детализацией по документам движения.
Настраивается отбор по произвольным полям. |
Предусмотрена настройка отбора по номенклатуре. |
| Отчет «Отчет по поступлению ГСМ» используется для анализа поступления нефтепродуктов одновременно в мере массы и мере объема в разрезе видов движения.
Настраивается состав выводимых в отчет показателей и полей, оформление отчета, отбор, сортировка и группировка по произвольным полям. |
упление ГСМ можно проанализировать с помощью стандартной бухгалтерской отчетности по счетам учета ТМЗ в разрезе доступных для счета субконто, либо по забалансовому счету «ДТ» в разрезе Пин-кодов и мест хранения нефтепродуктов. |
| Отчет «Отчет по расчету акциза» позволяет получить развернутую информацию о начислении акциза по реализованным нефтепродуктам.
Настраивается состав выводимых в отчет показателей и полей, оформление отчета, отбор, сортировка и группировка по произвольным полям. |
Предусмотрена настройка отбора по виду движения ГСМ, группировка по видам движения ГСМ, документам движения и Пин-кодам. |
| Отчет «Отчет по реализации» позволяет анализировать информацию по реализации ГСМ в разрезе видов движения, номенклатуры, Пин-кодов и т.д.
Настраивается состав выводимых в отчет показателей и полей, оформление отчета, отбор, сортировка и группировка по произвольным полям. |
Предусмотрена настройка отбора по номенклатуре, виду деятельности и контрагенту, группировка по виду деятельности. |
| Отчет «Реестр исходящих сопроводительных накладных» позволяет анализировать информацию по входящим сопроводительным накладным.
Настраивается состав выводимых в отчет показателей и полей, отбор и сортировка по произвольным полям, доступна группировка по виду нефтепродуктов. |
Предусмотрена настройка отбора по номенклатуре и контрагенту |
| Отчет «Реестр входящих сопроводительных накладных» позволяет анализировать информацию по входящим сопроводительным накладным.
Настраивается состав выводимых в отчет показателей и полей, отбор и сортировка по произвольным полям, доступна группировка по виду нефтепродуктов. |
Не предусмотрено |
| Ценообразование |
| Назначение цен на нефтепродукты производится за один килограмм и за один литр. Установка цен в первичных документах производится в соответствии с мерой ввода данных (объем или масса). |
Назначение цен на нефтепродукты производится для базовой единицы измерения номенклатуры. При установка цен в первичных документах не контролируется мера ввода данных (объем или масса). |
| Предусмотрена возможность указывать цены нефтепродуктов не только в целом для организации, но и отдельно для каждого места хранения (нефтебаза или АЗС) нефтепродуктов. |
Не предусмотрено |
| Учет талонов на отпуск нефтепродуктов через АЗС |
| Поштучный учет талонов |
| Ведется поштучный учет оборота талонов от момента реализации покупателю вплоть до погашения (отоваривания), а также учитывается объем реализованных по талонам горюче-смазочных материалов в количественно-суммовом выражении |
Учитывается объем реализованных по талонам горюче-смазочных материалов в количественно-суммовом выражении |
| Учет талонов ведется по номиналам, сериям и номерам, а также сроку действия талонов |
Не предусмотрено |
| Счета на талоны |
| Оформление счетов на предварительную оплату талонов для отпуска нефтепродуктов с АЗС |
Счета выставляются только на нефтепродукты |
| Списание бланков талонов |
| Предусмотрена возможность автоматически списывать со склада (места хранения) бланки при реализации талонов покупателям |
Не предусмотрено |
| Документооборот |
| При реализации талонов в бухгалтерском учете формируются проводки по отражению доходов будущих периодов и образованию дебиторской задолженности перед покупателем.
В оперативном учете отражаются детальные сведения о каждом реализованном талоне, в т.ч. марка топлива, номинал, серия и номер, срок годности, а также объем нефтепродуктов в количественно-суммовом выражении, подлежащих отпуску по талону |
При реализации талонов формируются проводки по забалансовому счету, отражающие объем подлежащих отпуску нефтепродуктов в количественно-суммовом выражении |
| Отражение в учете операций возврата приобретенных ранее талонов, не отоваренных по каким-либо причинам |
Не предусмотрено |
| Регистрация в учете факта погашения поступивших в бухгалтерию с автозаправочных станций талонов, по которым была произведена отгрузка нефтепродуктов покупателям |
Не предусмотрено |
| Учет погашенных покупателями талонов в разрезе АЗС |
Не предусмотрено |
| Отчетность |
| Настраиваемая отчетность для детального анализа запланированной отгрузки нефтепродуктов в различных разрезах и движения талонов (реализация, возврат, погашение) |
Анализ запланированного и фактически отгруженного объема нефтепродуктов по талонам с помощью стандартной бухгалтерской отчетности |
| Ответственное хранение |
| Документооборот |
| Удержание нефтепродуктов за услуги хранения, а также списание естественной убыли нефтепродуктов по хранению |
Не предусмотрено |
| Отражение в учете операций переоформления нефтепродуктов с одного хранителя на другого |
Не предусмотрено |
| Регистрация данных актов слива нефтепродуктов и формирование печатной формы «Акт приемки нефтепродуктов» |
Не предусмотрено |
| Регистрация результатов проведения инвентаризации нефтепродуктов, находящихся на ответственном хранении |
Не предусмотрено |
| Отчетность |
| Анализ поступления и отгрузки нефтепродуктов на ответственном хранении одновременно в мере массы и объема |
Не предусмотрено |
| Настраиваемая отчетность для детального анализа остатков и оборота нефтепродуктов, находящихся на ответственном хранении, в различных разрезах |
Анализ движения нефтепродуктов, находящихся на ответственном хранении, с помощью стандартной бухгалтерской отчетности |
| Отчетность для анализа дополнительных сведений о поступивших на хранение нефтепродуктах (номера цистерн, взлив, температура, плотность и т.д.) и отгруженных нефтепродуктах за определенный период (хранитель и договор хранителя, водитель и государственный номер транспортного средства, склад и т.д.) |
Не предусмотрено |
| Производство (переработка) |
| Передача в переработку |
| Отражение в учете операций передачи собственного сырья (нефти) в переработку стороннему производителю (НПЗ) |
Не предусмотрено |
| Поступление из переработки |
| Отражение в учете операций получения услуг по выпуску продукции сторонним переработчиком (НПЗ), самой продукции (нефтепродуктов) и отражения отчета об использованных материалах |
Не предусмотрено |
| Учет акциза |
| Учет по КБК |
| Учет расчетов с бюджетом по акцизу за реализованные нефтепродукты в разрезе произвольного количества кодов бюджетной классификации. Настройка пользователем порядка назначения кодов бюджетной классификации в бухгалтерских проводках по исчислению акциза. |
Для каждого вида подакцизного ТМЗ (бензин, дизельное топливо) может быть установлен только один код бюджетной классификации. |
| Декларация по акцизу, форма 400.00 |
| Автоматическое заполнение раздела «Исчислено акциза» приложения №5 «Облагаемые операции по бензину (за исключением авиационного), дизельному топливу» (форма 400.05). Исчисленная сумма акциза распределяется по кодам бюджетной классификации. |
Не предусмотрено |
| Панель функций |
| Панель функций наглядно показывает порядок работы в виде схем по наиболее часто используемым операциям. Также с помощью панели функций легко найти нужные учетные данные или отчеты. |
Есть только один способ найти требуемый документ или отчет – через меню. Для отражения в учете хозяйственной операции надо помнить, где в меню расположен нужный документ. |
| Дополнение к типовому решению |
| В качестве основы для разработки отраслевого решения «1С-Рейтинг:Нефтебаза» использовалась типовая конфигурация «Бухгалтерия для Казахстана», обладающая рядом существенных преимуществ, связанных как с использованием возможностей новой технологической платформы, так и с развитием функциональности и эргономики типового решения |
В качестве основы для разработки отраслевого решения «1С-Рейтинг:Нефтепродукты» использовалась типовая конфигурация «Бухгалтерский учет для Казахстана», уступающая в функциональности и эргономике своему аналогу на платформе «1С:Предприятие 8» |
| Следующая версия популярной программы |
| Конфигурация вобрала в себя все лучшее, что было реализовано в предыдущей версии (1С-Рейтинг:Нефтепродукты), и то новое, что создано с учетом опыта совместной работы с многочисленными пользователями и партнерами компании «1С-Рейтинг». |
Первая версия отраслевого решения для учета оптово-розничной реализации нефтепродуктов, хорошо зарекомендовавшей себя и являвшейся популярной на протяжении продолжительного периода времени. |
| Интеграция с другими программными продуктами |
| Поддерживается интеграция с конфигурацией «1С-Рейтинг: Налоговый мониторинг (МОП)», обеспечивающая возможность автоматического формирования наборов отчетов «Мониторинг крупных предприятий, субъектов рынка нефтепродуктов» и «Мониторинг крупных предприятий, хозяйствующих субъектов». |
В состав регламентированных отчетов включен набор отчетов «Мониторинг крупных предприятий, субъектов рынка нефтепродуктов». Набор отчетов «Мониторинг крупных предприятий, хозяйствующих субъектов» пользователям конфигурации не доступен. |
| В конфигурацию, в качестве подсистемы управления затратами на автотранспорт, интегрировано отраслевое решение «1С-Рейтинг: Управление затратами на автотранспорт. Путевые листы».
Подсистема позволяет вести полноценный учет движения ГСМ по путевым листам на транспортных средствах (ТС) предприятия, выработки ТС и водителей, шин и аккумуляторов, выполнять расчет зарплаты водителей.
Для работы с подсистемой управления затратами на автотранспорт необходимо приобрести лицензию на прикладное решение «1C-Рейтинг: Управление затратами на автотранспорт. Путевые листы». |
В конфигурацию включен документ «Путевой лист», предназначенный для списания ГСМ на производственные, административные и прочие затраты предприятия. |
| Переход с «1С-Рейтинг: Нефтепродукты» 7.7 |
| Для пользователей «1С-Рейтинг: Нефтепродукты», ред. 2.0 облегчен переход на новую версию программы. Данные для начала ведения учета в «1С-Рейтинг: Нефтебаза» могут быть автоматически перенесены из «1С-Рейтинг: Нефтепродукты». |
Предусмотрена процедура выгрузки данных для перехода на «1С-Рейтинг:Нефтебаза». |
| Специальная цена для пользователей «1С-Рейтинг: Нефтепродукты» 7.7 |
| Для пользователей учетного решения предыдущей версии предусмотрена льготная цена (апгрейд) при приобретении «1С?Рейтинг:Нефтебаза 8». Льготная цена составляет: стоимость «1С?Рейтинг:Нефтебаза 8» минус стоимость заменяемой программы плюс 750 тенге, но не менее половины стоимости приобретаемого продукта.
Полный прайс-лист — http://1c-rating.kz/programs/industry-solutions/price.php |
Апгрейд на решения версии 7.7 не производится. |
| Развитие программы |
| «1С-Рейтинг:Нефтебаза» развивается с 2007 года. За это время выпускались редакции программы, учтены многочисленные пожелания и замечания пользователей. На сегодняшний день «1С-Рейтинг:Нефтебаза» успешно работает в организациях самого разного масштаба и продолжает развиваться. Основные направления развития – расширение функциональных возможностей и повышение удобства работы пользователя. |
Отрабатываются только изменения законодательства. Разработка новых возможностей не ведется. |
| Система защиты и лицензирования |
| Использование сетевого ключа защиты на определенное число лицензий |
Установка ключей защиты на каждую рабочую станцию |
| Возможность наращивания количества лицензий путем подключения дополнительных сетевых ключей к серверу |
Не предусмотрено |
| Поддержка 64-х разрядных ОС |
Не предусмотрено |
| Возможность запуска сетевого сервера в режиме службы |
Не предусмотрено |
| Возможность работы системы в локальных сетях, состоящих из нескольких сегментов |
Не предусмотрено |
| Возможность обслуживания сервером нескольких защищенных продуктов |
Не предусмотрено |
| Использование протокола TCP/IP для связи |
Использование протокола NetBIOS для связи |
| Масштабируемость и производительность |
| Эффективная работа и надежное хранение информации при работе десятков и сотен пользователей.
«1С:Предприятие 8» поддерживает как файловой вариант работы, так и клиент-серверный вариант. При переходе к технологии «клиент-сервер» не требуется вносить изменения в прикладное решение (одни и те же прикладные решения могут использоваться в обоих вариантах).
http://v8.1c.ru/overview/Power.htm
Современная архитектура информационной системы обеспечивает сохранение высокой производительности при значительном росте нагрузки на систему и объемов обрабатываемых данных и позволяет увеличивать пропускную способность путем наращивания мощности используемого оборудования без затрат на модификацию или замену конфигурации. |
При увеличении количества пользователей (до нескольких десятков) может происходить падение производительности. |
| Средства разграничения прав доступа |
| Прикладное решение содержит механизм ограничения прав доступа пользователей на основе механизма ролей, который позволяет скрыть конфиденциальную информацию и предоставить пользователю доступ только к тем данным, которые необходимы для его работы.
Права доступа к данным могут быть определены с детализацией до отдельных записей либо даже отдельных полей этих записей. Например, пользователю можно разрешить оперировать документами (накладными и т.д.) только по определенным складам, не предоставляя ему доступ к аналогичным документам других складов; в доступных документах можно разрешить оперировать только определенными значениями и т.п. |
Права доступа определяются только на уровне объектов метаданных и расширяются системой полномочий. |
| Интеграция с другими системами |
| Новый уровень интеграции позволяет обеспечить оперативный обмен данными. При этом обмен можно производить только требуемыми (не всеми) данными, есть возможность трансформации данных, также возможно настроить автоматический обмен по заданному графику.
В результате создается единое информационное пространство, в каждой точке которого может применяться подходящее прикладное решение.
Прикладное решение содержит механизмы обмена данными с другими решениями на платформах «1С:Предприятие 8» и «1С:Предприятие 7.7» (реализован универсальный механизм обмена данными в формате XML).
Платформа «1С:Предприятие 8» предоставляет средства интеграции прикладного решения практически с любыми внешними программами и оборудованием на основе общепризнанных открытых стандартов и протоколов передачи данных.
В одном прикладном решении может быть создано несколько независимых схем обмена с различными системами. |
Предусмотрена только «ручная» (с помощью специальных обработок) выгрузка и загрузка данных из других решений. |
| Администрирование |
| Современные средства для более быстрого и удобного внедрения и сопровождения системы (в том числе ИТ-специалистами предприятия).
Динамическое обновление системы без прерывания работы пользователей.
В системе поддерживает мониторинг действий пользователей и регистрация системных событий. |
Блокирование работы пользователей при обновлении, отсутствие развитых средств мониторинга работы пользователей. |
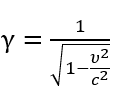
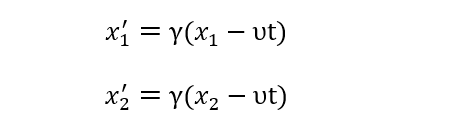
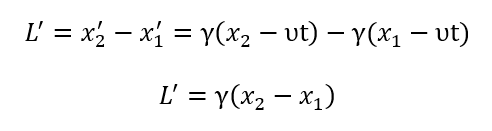
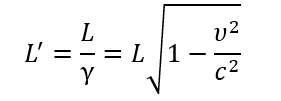


 1С: Бухгалтерия 8 для Казахстана. Учебная версия.
1С: Бухгалтерия 8 для Казахстана. Учебная версия.